Chapter 2- Application of Theories Flashcards
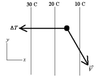
Horizontal divergence can be expressed as:
to compute horizontal divergence at (x0, y0) evaluate the derivative using the
central finite differences:
Example-1: Calculate the horizontal divergence for the data given in Figure. Given:
∆x=∆y=50km
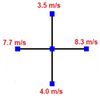
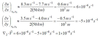
Example-1: Calculate the horizontal divergence for the data given in Figure. Given:
∆x=∆y=50km
Example-2: Repeat the above calculations with small changes (errors) in winds.
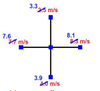
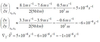
Divergence estimates using kinematic method areDivergence estimates using kinematic method are
very sensitive to small errors
Vorticity is a
microscopic measure of rotation at any point in a fluid
Vorticity is a microscopic measure of rotation at any point in a fluid. It may be considered to be
the local rotation of a fluid
Vorticity is a microscopic measure of rotation at any point in a fluid. It may be considered to be the local rotation of a fluid. Vorticity is a
vector field, which is defined as the curl of velocity
w=-/x V
where v =
(iu+ jv+ kw) is a 3d velocity field
-/x V =
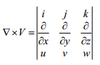
w=
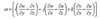
Because horizontal winds are usually larger than
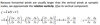
Relative vorticity has units of
of s-1 and vorticity is defined as positive in the counterclockwise direction
The Earth is rotating about its axis at rate
Ω (s-1).
Since winds are defined
relative to the Earth’s surface, we express rotation about the Earth’s axis, in terms of those same coordinates, as:
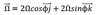
The vertical component of Earth vorticity is called the
coriolis parameter, f
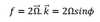
Absolute vorticity is
the vector combination of relative vorticity (ζ) and Earth vorticity (f):
ζa = ζ +f
absolute vorticity of a fluid parcel is equal to
the sum of the (vertical) rotation of the fluid parcel relative to the earth (relative vorticity) and the vertical component of the rotation of the earth at that position.
The gradient of a variable is
just the change in that variable as a function of distance
The gradient of a variable is just the change in that variable as a function of distance. For instance,
the temperature gradient is just the temperature change divided by the distance over which it is changing: /_\T//_\ distance
The gradient is a
vector and has a direction as well as magnitude.
Mathematically, the gradient vector is defined by
for example
The gradient of a scalar is
a vector whose direction is always normal to the isolines (contours) and pointing in the direction of increase
We can define the normal vector, which is just the
unit vector in the direction of the increasing temperature. We will call this normal vector n
The magnitude and direction of a 2D gradient vector for T can be determined by:
…………………………………….. then the gradient is zero
If the scalar is uniform in space
Advection
The transport of an atmospheric property (e.g., temperature, humidity), which is variable in space, by wind is called ‘advection’.
The transport of an atmospheric property (e.g., temperature, humidity), which is variable in space, by wind is called ‘advection’.
This transport process plays a very important part in
local changes of temperature and moisture, among other atmospheric properties
Mathematically, advection is expressed as:
Theoretically advection can be viewed as
three dimensional
Theoretically advection can be viewed as three dimensional. In operational
meteorology the term advection is typically limited to
transport by the horizontal flow while vertical transport is called convection
In Cartesian coordinates, horizontal advection is given by
Example: The wind is from 330° at 25 m/s. The isotherms are oriented north-south as shown in the picture below, and are 100 km apart.
For a thin layer, the geostrophic temperature advection is given by:
Troughs
Troughs which are the regions of low pressure are produced by large volumes of cool or cold air while large volumes of warm or hot air produce ridges, which are the regions of high pressure.
The winds on upper level charts blow
parallel to the contour lines generally from west to east
The winds on upper level charts blow parallel to the contour lines generally from west to east.
This is a little difference from
surface winds which blow across the isobars toward low pressure
Temperature drops as you move from
west to east and from south to north
For example, the highest point on the 850 mb surface (………….. m or so) is found above
1800
the hot air near the SW corner
For example, the highest point on the 850 mb surface (1800 m or so) is found
above the hot air near the SW corner. The lowest point
(a little less than 1000 m) is found in the coldest air near the NE corner of the picture.
The above distribution of height contours can be explained by noting that:
(1) pressure decreases with increasing altitude, and
(2) pressure decreases more rapidly in cold high-density air than it does in warm low-density air.
The counterclockwise winds spinning around the LOW move
warm air northward and cold air southward
The counterclockwise winds spinning around the LOW move warm air northward and cold air southward.
Warm air is found
west of the HIGH and to the east of the LOW. This is where the two ridges on the upper level chart are also found.
Warm air is found west of the HIGH and to the east of the LOW. This is where the two ridges on the upper level chart are also found.
Similarly, cold air is found
below an upper level trough.
The yellow Ox marked on the upper level chart directly above the surface L is
a good location for a surface LOW to form, develop, and strengthen (strengthening means the pressure in the surface low will get even lower; this is also called “deepening”).
The reason for this is that the yellow Ox is a location where there is often
upper level divergence
Similarly, the pink Ox is where we often find
upper level convergence
Similarly, the pink Ox is where we often find upper level convergence. this causes
the pressure in the center of the surface high to get even higher.
The area around a jet streak can be divided into four quadrant relative to the
it can be shown dynamically that for …………………………………….. are areas of divergence
straight flow in the upper troposphere, the left front and right rear quadrants (C and D)
are areas of divergence while …………………………….. are areas of convergence
right front and left rear quadrants (D and A)
Areas of divergence in the upper troposphere are typically associated with
upward synoptic scale vertical motion
area of upper level convergence are typically associated with
downward synoptic scale vertical motion
Where upper level convergence occurs air
sinks to promote high pressure at the surface.
Where upper-level divergence occurs air
is pulled up from the surface to help create low pressure near the ground.
Wave cyclones dissolve when
they no longer have the upper level divergence to maintain them
The combination of rising and sinking air creates
direct and indirect circulations in the rear (AB) and front (CD) regions across the jet stream, respectively
Because cyclones need ………………… to maintain themselves
divergence in the upper troposphere
Because cyclones need divergence in the upper troposphere to maintain themselves, the divergence/convergence regions around the jet streak have
direct affect on the surface lows and highs
The vorticity pattern associated with a (straight flowing) jet streak show
a strong positive relative vorticity maximum to the left of the jet maximum (plus) and a weaker negative relative vorticity minimum to the right ( minus).
The location of the vorticity maximum and minimum indicate that there should be
positive vorticity advection (PVA) in the left exit and right entrance regions.
Quasi-geostrophic theory indicated the PVA is favorable for
cyclone development.
Hence, the typical location of a intensifying surface low center is in
the left exit region
while …………………………. are common in the right entrance region.
newly formed frontal waves
A jet streak moves
within the trough-ridge pattern at the same time it influences the amplification or de-amplification of the trough-ridge pattern.
Below is an example of a jet streak de-amplifying (weakening) a trough
A strong jet streak on the right side of a trough will cause that trough to de-amplify (lift)
amplifying (image)
If a strong jet streak is on the left side of a trough, the trough will amplify (dig)
