Chapter 13: Relationships Flashcards
How do you test a correlation coefficient using z-scores? Run yourself through the procedure.
You need two values: the signal and the error.
Signal: Use the Zr formula from below (practice reciting it).
Noise: Use the SE formula with an additional -3 [σ/sqrt(N-3)]
Test-Statistic: Divide your signal by your error.
Now look-up your value in a z-score chart.
What units are the standardized residual values in? Because of this, how can we evaluate their significance?
The standardized residual values are z-scores.
We can evaluate these residuals by comparing them to z-score significance values.
z > 1.95 = significant at 0.05
z > 2.58 = significant at 0.01
z > 3.29 = significant at 0.001
Is covariance normalized or standardized?
Normalized.
What is a common complaint against the Yate’s correction?
It tends to over-correct the test-statistic, resulting in too low of a value.
How can you transition a covariance value into a correlation coefficient?
You divide covariance by the product of both groups standard deviations.
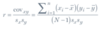
What do the words ‘Tertium Quid’ mean?
An unaccounted variable affecting the measurement (a confound).
When would you use the ‘likelihood ratio test’ (G-test)?
As an alternative to the chi-squared test for when sample sizes are small.
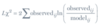
Explain the process of calculating confidence intervals for correlation coefficients.
You start by calculating the lower and upper boundary for your confidence interval.
Zr±(1.96*SEZr)
These are the same values that you used to calculate your z-score test statistic.
Take the upper and lower bound then plug them each into the attached formula.
Does your range contain zero?
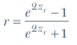
What does a Bayes Factor tell you?
“The Bayes factor tells you the probability of the data given the alternative hypothesis relative to the probability of the data given the null hypothesis.”
Covariance might otherwise be called the average cross-product deviation. What is the formula for covariance, and why does the first sentence make sense?
The top part of this formula is called the cross-product deviation–the residual for each factor multiplied. We then sum the cross-product deviation for each datum to get the sum of cross-product deviations.
The sum of cross-product deviations becomes covariance when it is divided by the degrees of freedom–(N-1). This, mathematically, is akin to taking an average cross-product deviation across your data set.
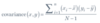
You receive a chi-square value of -4, what can you derive from this?
The calculations were done incorrectly. Given that you square the residual a negative outcome is not possible.
When and how would you conduct a Yate’s correction?
You would conduct a Yate’s correction on a 2x2 table that has low expected frequencies.
This uses roughly the same formula as a chi-squared test except that your residual is an absolute value that has 0.5 subtracted from it.
What is a percentage bend correlation?
A non-linear correlation line that is robust to outliers and extreme cases.
What does a Pearon’s chi-square test evaluate? And what is the default assumption?
Checks whether there is a relationship between two categorical variables. Assumes that there is no relationship (the null hypothesis).
What rules must we follow with a 2x2 contingency table? What about a larger table?
2x2 tables must not have an expected value of lower than 5.
Contingency tables larger than 2x2 must have no more than 20% of its square with a value less than 5, and all with a value above 1.
What is the chi-square formula? What does each of these variables contribute to said formula?
Observed: The value that was observed for the condition.
Model: The value that represents the null hypothesis for the condition.
Squaring The Difference: Squaring the difference of the observed and model values removes negative inputs.
Divide by Model: Dividing by the expected value standardizes the results.
How do you calculate the standardized residual? Why is this value useful?
You use the pure deviation version of the chi-squared formula, except that your standardization (model/expected value) is squared.
This is useful because it provides you with the individual residual contributions to the chi-squared value. Meaning, if you add each standardized residual then you get the chi-squared test-statistic.
How do you calculate an expected frequency for a contingency table? What hypothesis does this represent?
Using the formula below.
The expected frequency represents the frequency of an event that you would expect if there was no relationship between two variables–i.e. the null hypothesis.
How do you test a correlation coefficient using a t-distribution? Run yourself through the procedure.
Simply use the formula below.
Take your test-statistic to a t-chart and check for significance.
If your value is bigger than the one listed then it is significant.
If your value is smaller than the one listed then it is not significant.
