Chapter 11: Modern Approaches to Theory Testing

Question 1

What fundamentally different questions do NHST and Bayes Theorem ask?

Answer 1

NHST: What is the probability of my test statistic (data) given that the null hypothesis is true?

Bayes: What is the probability of the alternative hypothesis being true given the data?

Question 2

In the Bayes Theorem, what term represents our data or evidence?

Answer 2

Marginal likelihood.

Question 3

Why might looking at confidence intervals be more advantageous than p-values?

Answer 3

“If you look at the confidence intervals rather than focusing on significance it allows you to see the consistency in the data–rather than the conflicting results implied by the NHST approach.”

Question 4

What are the three measures of effect size that we discussed in this chapter?

Answer 4

1) Cohen’s d. 2) Pearson’s correlation coefficient r. 3) Odds ratio.

Question 5

Assign a term to each part of Baye’s Theorem.

Answer 5

Question 6

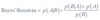
In a situation where your sample sizes are highly discrepant should you use Cohens’ d Pearson’s r?

Answer 6

“…when group sizes are very discrepant r can be quite biased compared to d.”

Question 7

What types of variables must we use Pearons’s r on?

Answer 7

Pearson’s r must be used with either a single continuous variable and a categorical variable or between two continuous variables.

Question 8

Differentiate a confidence from a credible interval.

Answer 8

Confidence Interval: 95% of all trials will fall in this range (long-run probability)

Credible Interval: There is a 95% chance that the trial will fall in this range (single trial statement)

Question 9

What should be the first thing that you check when looking at a confidence interval?

Answer 9

If the range contains zero. This indicates the possibility of no-true effect.

Question 10

How do we calculate Cohen’s D?

Answer 10

Subtract group means then divide by the standard deviation.

d = X₁-X₂/Sigma

Question 11

Pearson’s r is not measured on a linear scale. What does this mean for data interpretation?

Answer 11

This means that results cannot directly be compared. For example, you cannot say that r = 0.8 is twice as large as r = 0.4.

Question 12

For each of these questions, which standard deviation would you use to compute Cohen’s d?

1) Control: s = 6

Experimental: s = 7

2) Experimental 1: N = 18; s = 9

Experimental 2: N = 14; s = 13

Answer 12

1) You would use the standard deviation for your control group, 6.
2) You must compute a pooled standard deviation, 10.9.

Question 13

At which levels would you classify a Cohen’s d value as either small, medium, or large?

Answer 13

d = 0.2 = small

d = 0.5 = medium

d = 0.8 = large

Question 14

How are effect sizes impacted by sample size?

Answer 14

Sample size does not affect effect size.

Question 15

What type of data would we use an odds ratio for?

Answer 15

Frequency data, which includes categorical data. I.e. trying to determine the likelihood of two events relative to each other.

Question 16

At which levels would you classify a Pearson’s r value as either small, medium, or large?

Answer 16

r = 0.1 = small

r = 0.3 = medium

r = 0.5 = large

Question 17

What are the major arguments against NHST?

Answer 17

1) Significance does not equate to importance. 2) The null hypothesis can always be falsified if you have a large enough sample size. 3) Confidence intervals encourage an all-or-nothing mindset. 4) Experimenter intention changes the required p-value.

Question 18

What units does Cohen’s d report in?

Answer 18

Standard deviations.

Question 19

What is a Bayes Factor? What values of it qualify for our interest?

Answer 19

Bayes Factor: The probability of the data given the alternative hypothesis is x times more likely than the probability of the data given the null hypothesis.

<1: Null hypothesis more probable.

1-3: Alternative hypothesis more probable, but not worth mentioning.

3-10: The alternative hypothesis evidence is substantial.

Question 20

What are some of the advantages of Bayes Theorem over NHST?

Answer 20

1: Hypothesis tests probabilities based on available data, and not long-run probabilities.
2) Provides evidence on whether the null hypothesis is true.
3) Sample size does not skew inference, only increases the amount of evidence.
4) Do not need to pre-determine N.
5) Does not rely on an arbitrary significance criterion.

Question 21

The error values that we use for NHST are based on what type of probability?

Answer 21

Empirical, long-run probability. The assumption that these values would only come to be if the experiment was replicated an infinite number of times.

Question 22

How do you calculate posterior odds, and what do they tell you?

Answer 22

By dividing the posterior probability of hypothesis 1 over hypothesis 2. This, in effect, gives you an odds ratio of hypothesis: how much more likely one hypothesis is over the other.