Chapter 10 Flashcards
(20 cards)
What must be established to use a two-sample test that compares the
means of samples selected from two populations
You must establish whether the assumption that the variances in the two populations are equal holds.
The statistical method used to test whether the means of each population are different depends on whether the assump-tion holds or not.
Define a pooled-variance t test
A pooled-variance t test is used to determine whether there is a significant difference between 2 means
You must assume
- that the random samples are independently selected from two populations and
- that the populations are normally distributed and have equal variances
What is the equation for a pooled-variance t test for the difference b/t 2 means
see image
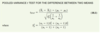
Define the variables of a pooled-variance t test
see image

Review Regions of Rejection and Nonrejection
see image 3

How do you check for normality in each of the two populations of a pooled-variable t test
Use a box-plot
What is the equation to determine the confidence interval estimate for the Difference between two Means
see image 4

When do you use the separate-variance t test
When
- You can assume that the two independent populations are normally distributed BUT
- You cannot assume that they have equal variances (S2)
What are two situations that involve related data
- When you take repeated measurements from the same item
- When you match items or individuals according to some characteristic
In either situation, your are interested in the difference between the two related values rather than the individual values themselves
What must you assume when you take repeated measurements
You assume the same items or individuals will behave alike if treated alike
What is the goal when comparing the means of two related populations
To show that any differences b/t two measurements of the same items or individuals are due to different treatments that have been applied to the items or individuals
Review Table for the Differences b/t Individual values for two related populations
see image 5

When do you use the Paired t test for the mean difference
If you assume that the different scores are randomly and independently selected from a population that is normally distributed
Define the equation for the Paired t test for the mean difference
see image 6

Define the confidence interval estimate for the mean difference
w/ equation
To construct a confidence interval estimate for the population mean difference
see image 7

Comparing the Proportions for Two Independent Populations
Use the test statistic ZSTAT
Define the Z Test for the Difference Between Two Proportions w/ equation
Based on the difference between to sample proportions (p1 - p2)
See image 8

Define the Confidence Interval Estimate for the Difference Between Two Proportions
see image 9

Define the F Test for the Ratio of Two Variances
- Often you need to determine whether two independent populations have the same variability.
- By testing variances, you can detect differences in the variability in two independent popu-lations.
One important reason to test for the difference between the variances of two populations is to determine whether to use
- the pooled-variance t test (which assumes equal variances)
- or the separate-variance t test (which does not assume equal variances) when comparing the means of two independent populations
Define the Equation for the F Test Statistic for Testing The Ratio of Two Variances
See image



