Chap 4c - Circular Motion Flashcards
CM stands for ____ ____
AND
LM stands for ____ ____
Circular Motion
AND
Linear Motion
It is easy to memorize the CM equations because they are exactly parallel to the _____________.
Linear Motion Equations
In linear motion, position is “x.” In CM angular position is_
theta
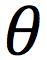
All points on a rotating wheel will have the same ________
Angular Velocity (they would also have the same angular acceleration, if any)

What is the difference between a positive and a negative angular velocity?
The direction the particle is travelling around the circle.
counterclockwise = positive.
clockwise = negative
angular position
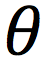
The angle of a particle from the positive x-axis

The area under an angular acceleration graph is_
The change in angular velocity.
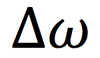
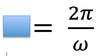
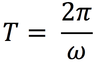
“v “ in LM
is like ___ in CM
omega
(angular velocity)
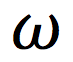
In circular motion, the symbol we will use to represent the period.
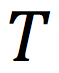
The slope of an angular velocity vs. time graph is_.
The angular acceleration
(alpha)
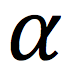
The equation below is for LM. What is the analogous equation for CM

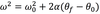
“a” in LM
is like ____ in CM
alpha
(angular acceleration)
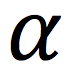
In CM,

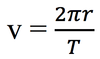
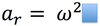
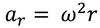
Uniform circular motion
Moving at a constant speed around a circle of radius “r”
The equation below is for LM. What is the analogous equation for CM
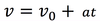

What is the Greek symbol for Omega?
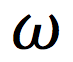
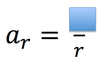
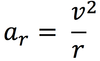
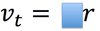
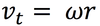

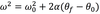
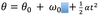
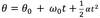
tangential acceleration
the acceleration parallel to the velocity of an object travelling in a circular path.
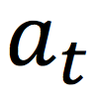

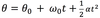
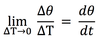
angular velocity
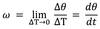
One radian is approximately ______ degrees.
60 degrees
(57.296)
The area under an angular velocity graph is_
The change in angular position.

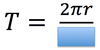
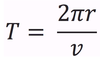
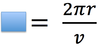
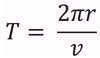
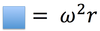
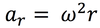
LM to CM
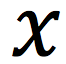
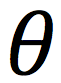
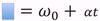
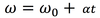
By convention, which way around a circle is typically considered positive?
Counterclockwise
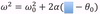
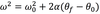
How many radians are there in one full revolution
There are 2π radians in one full revolution.
Nonuniform circular motion
Circular motion with a changing speed.

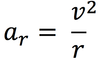
centripetal acceleration
acceleration perpendicular to the motion of an object and toward the center of a circular path.
A negative angular acceleration could mean speeding up in the clockwise direction or_.
Slowing down in the counter clockwise direction.

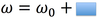
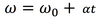
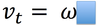
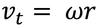
The slope of an angular position vs. time graph is_
The angular velocity.

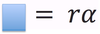
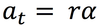
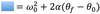
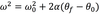
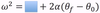
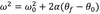
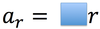
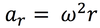
In circular motion, the velocity of the particle is always _______ to the circle.
Tangent
radial acceleration is also known as
centripetal acceleration
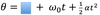

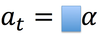
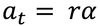
The time required for a particle to make one complete trip around the circle is called a…
Period

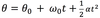
LM to CM
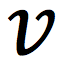

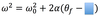
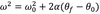
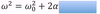
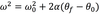
crankshaft
a rotating rod in the engine of a car.
(Actually, its a bit more complicated than this, but all you need to know is that it is a rod and it rotates)

The rate at which a particle’s angular position is changing as it moves around a circle.
Angular Velocity

Delta Theta divided by Delta T =

average angular velocity
In circular motion, the angle measured between a particles starting position and ending position is called_
Angular displacement (delta theta)

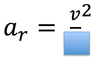
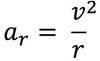
There is one equation that is pretty much responsible for why we use “radians” instead of degrees. What is it?
(In the equation below, “s” is just a measure of the distance you travel around the edge of a circle.)
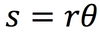
A particle is in _________ if an only if its angular velocity is constant and unchanging.
Uniform Circular Motion
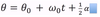
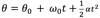
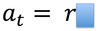
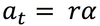
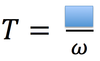
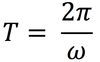
rpm
revolutions per minute
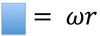

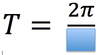
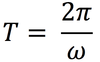
For the equation below to work, the angle must be measured in ___________
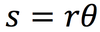
radians.
Points on a rotating wheel can have different_
Tangential velocities (they might also have different tangential accelerations)
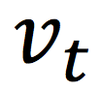

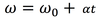

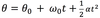
LM to CM

alpha

The equation below is for LM. What is the analogous equation for CM
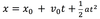
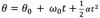

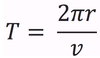
A positive angular acceleration could mean speeding up in the counter clockwise direction or_.
Slowing down in the clockwise direction.

What is a “degree,” and who invented them?
A degree is 1/360th of the way around a circle. You can thank the Babylonians for this.
(The numbers 6 and 60 had religious significance, and 6 x 60 = 360, so…. you know that’s pretty neat)
What are radians?
A radian is the angle swept out by an arc that has a length equal to the radiius of the circle.
It is neat because it makes sense.
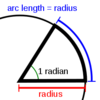
Why do we use radians?
All the math works out easily when you use radians.
Why don’t we use “degrees” in circular motion?
If you try to use degrees in circular motion, you end up having to multiply stuff by 2π/360 all the time to make it work. It gets kind of old.
Remember, degrees don’t really mean anything. I guess they did to the Babylonians, but they are dead now.
Radial Acceleration is also known as:
ar
Centripital Acceleration
ac
In uniform circular motion, the force applied is always…
**perpendicular to the direction the object is moving. **
(and toward the center of the circle)


