AP Electricity and Magnetism Equations to memorize Flashcards
Rotational instantaneous power
P = τ·ω
Electric field of a point charge
E = kq / r2
Ampere’s law
μ0I = ∫(B)(ds)
Integral of a differential
∫ dx = x + C
Centripetal acceleration based upon v
ac = v2 / r
Lenz’s law
The current induced by a changing magnetic flux creates a field which opposes the change
Energy in an inductor

Newton’s third law
Fab = -Fba
Impulse for a constant force
J = (ΣF)(Δt)
(Impulse = force x time)
Area under a force/time function
Impulse
Instantaneous power
P = F∙v
Energy in a capacitor (3)
U = ½QV = ½CV2 = ½Q2/C
Derivative chain rule
d/dx (u) = (du / dv)(dv / dx)
Resistors in series
Rseries = R1 + R2 + R3 ….
Spring force
Fsp = -ks
Derivative quotient rule
d/dx (u / v) = (1/v)(du/dx) – (u/v2)(dv/dx)
Relative motion
va,c = va,b + vb,c
Center of mass
rcm = (m1)(r1) + (m2)(r2) … / Σm
Rule for the angle of the cross product
Rotate counterclockwise from the first vector to the second vector
Conservation of angular momentum
I1ω1 = I2ω2
Centripetal acceleration based upon ω
ac = ω2R
Relationship between the force and the change in energy per unit distance.
F = -dU/ds
This is a combination W = f x d and W = -ΔU
Work – potential energy relationship
-W = ΔU
Resistance of a wire
R = ρ(L/A)
Where ρ is resisitivity
L = length
A = cross sectional area
Magnetic field of a straight wire
B = μ0I / 2πR
vf2 equation
vf2 = vi2 + 2(a)(Δs)
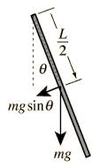
Force down an incline
Fll = Fg ∙ sinθ
Gravitational potential energy on a planet
Ug = mgh
Rotational inertia of point masses
I = Σ(mr2)
Slope of a velocity/time graph
Acceleration
Torque (2)
τ = F∙ r┴
( torque = force times “lever arm” )
(The lever arm is just the shortest distance between the axis of rotation and the path the force is acting along.)
Cartesian to polar coordinates (2)
v = √(vx2 + vy2)
Rotational work
Wrot = (τ)(Δθ)
Integral of an exponential term
∫ (eu)dx = (1/u’)(eu) + C
Describe the electric field inside a conductor
Electric charge and field are zero
Voltage across an inductor
V = -L(dI / dt)
Battery emf
EMF = V - IRint
Magnetic flux
ФB = A∙B = ABcosθ
(Often, in the problems we do, the area vector and the magnetic field will be parallel, so the cosθ is equal to one and thus dropped from the equation.)
Resistors in parallel
1/Rparallel = 1/R1 + 1/R2 + 1/R3….
Centripetal force
Fc = mac
Period of a simple pendulum
T = 2π√(L/g)
Kinetic friction
Fkf = ± μkf∙ FN
Integrating with a constant
∫ k f(x)dx = k ∫ f(x)dx
Period of a physical pendulum
T = 2π√(I/mgd)
Power in a circuit (3)
P = IΔV
Electric potential (general)
V = U / q
Displacement under constant acceleration
Δs = (vi)(Δt) + ½(a)(Δt2)
Electrostatic force between point charges
FE = kq1q2 / r2
Acceleration due to gravity
g = G∙mp/rp2
(This is pretty much just the Law of Universal Gravitation with the mass of the planet and the radius of the planet plugged in.)
RC circuit growth
Vc = Vs(1e-t / RC)
RC the time constant (tau) (resistance x capacitance)
Vs is the supplied voltage
Law of Biot-Savart

Gravitational potential energy in space
Ug = (-G∙m1∙m2)/ r
Universal force of gravity
Fg = (G∙m1∙m2 )/ r2
Acceleration
a = dv / dt
Slope of a potential energy / position graph
Negative of force
Power input by a force
P = W / Δt
Electric flux
ФB = E∙A
( In most cases that we will work with at this level, the two will be perpendicular, so the dot product just drops out. )
Area under an acceleration/time function
Change in velocity
Sum rule for integration
∫ (u + v)dx = ∫ (u)dx + ∫ (v)dx + C
Derivative of sin
d/dx (sin x) = cos x
Area under a force/position function
Work
Escape velocity
v = √2Gm / R
Kinetic energy
K = ½ mv2
Inductance

Constant acceleration
a = Δv / Δt
Derivative of cos
d/dx (cos x) = - sin x
Derivative of exponential terms

RH open palm rule for force on a moving charge
Thumb - direction charge or current is moving
Fingers - direction of magnetic field
Open palm - direction of force.
Displacement
Δs = sf – si
Potential energy in a spring
Usp= ½ ks2
Force between two wires

Integral of sin
∫ (sin x)dx = -cos x + C
Horizontal vector component
vx = v(cos θ)
Formula for finding initial vertical velocity of a projectile given its initial velocity and angle at which it is fired.
vy = v(sin θ)
Capacitance (2)
C = ε(A/d)
ε = permeativity of free space (8.85 x 10-12 F/m)
Relationship between electric potential and electric field.
dV = -E·ds
Force in a gravitational field
Fg = -mg
Power rule for integration
∫ f(xn)dx = (xn+1/n+1) + C
Conservation of angular momentum
ΔL=0
if and only if
Στext = 0
Faraday’s law of induction
EMF = -N(dФB / dt)
( N is the number of loops )
Rule for the angle of the dot product
Rotate counterclockwise from the first vector to the second vector
Work done by a variable force
W = ∫(F)(ds)
Newton’s second law for rotation
Στ = I∙α
( α is alpha, or angular acceleration )
Momentum
p = mv
Rotational kinetic energy
Krot = ½∙I∙ω2
Magnetic force on current-carrying wire
F = IL x B
Integrating 1/x
∫ (1/x)dx = ln|x| + C
Angular momentum (2)
L = rmv
also
L = Iω
Impulse equation
J = Δp
( Impulse = change in momentum )
Satellite velocity
vsat = √(G∙mcenteral / rorbit)
Slope of a momentum/time graph
Force
Derivative sum rule
d/dx (u + v) = du/dx + dv/dx
Relationship between period and frequency
T = 1/f
RC circuit decay
Vc = Vi(e-t / RC)
RC the time constant (tau) (resistance x capacitance)
Vi is the intital voltage on the capacitor
Static friction
Fsf ≤ ± μsf ∙ FN
Integral of cos
∫ (cos x)dx = sin x + C
Work (2)
W = (Fll)(Δs)
Work – energy theorem
ΣW = ΔK
( make sure you remember this one )
Velocity
v = ds / dt
Gravitational field lines
Vectors point how a test mass would accelerate
Electric current
I = dQ / dt
Parallel axis theorem
I = Icm + md2
( If you know the moment of interia of an object rotating around its center of mass Icm but the object is instead rotating around an axis that is distance “d” from the center of mass, the new rotational intertia can be found with this equation )

Average velocity
vavg = Δs / Δt
Area under a velocity/time function
Change in position
Conservation of energy
ΣU + ΣK + ΣEth = constant for a closed system
( this is a simplification, as it does not include chemical potential energy, electrical potential energy, etc. )
Derivative power rule

Period of a spring oscillator
T = 2π√(m/k)
RL circuit decay
VL = V0(e-Rt / L)
Magnetic force on a moving charge
F = qv x B
Speed
S = distance / time
Kirchhoff’s rule
ΔVloop = 0
Capacitance with a dielectric
C = κε(A/d)
κ = dielectric constant

Impulse for a variable force
J = ∫(F)(dt)
Gauss’s law for permanent magnets
ФB = 0
Newton’s second law
ΣF = ma
(don’t forget how many times you could get 1 point on a free response simply by writing this down)
Angular frequency (2)
ω = 2πf
Slope of a position/time graph
Velocity
Average velocity when acceleration is constant
vavg = (vi + vf ) / 2
Ohm’s law
ΔV = IR
Force perpendicular to an incline
FN = Fg ∙ cosθ
Electrostatic potential energy of two point charges
UE = kq1q2 / r
Electric field (general)
E = F / q
Capacitors in series
1/Cseries = 1/C1 + 1/C2 + ….
Electric potential of a point charge
V = kq1 / r
Conservation of momentum
Σpi = Σpf if ΣFext = 0
( With no external forces, the momentum of a system will be conserved )
( This is true for both linear and angular momentum )
Electric field lines
Vectors pointed how a positive test charge would accelerate
Power (general)
P = ΔE / Δt
Capacitors in parallel
Cparallel= C1 + C2 + C3 ….
(Note: this is sort of opposite the rule for resistors in parallel. )
Derivative product rule
d/dx (uv) = v(du/dx) + u(dv/dx)
RH curl rule for a wire’s magnetic field
Point RH thumb in the direction of the current, RH fingers curl in the direction of the resulting magnetic field.
Rotational inertia of radially symmetric objects
I = kMR2
( k = the number of these objects )
Gauss’s law
Qenc = ε0ФE
Equations for rolling (3)
ds = r∙dθ
Time constant for RC circuit
τ = RC
τ is tau
R = resistance
C = capacitance


