Algebra I Flashcards
1
Q
What is a Geometric Sequence?
A
- a sequence with a constant increase or decrease involving multiplication or division
- each term is found by multiplying the previous term by a constant
- 2, 4, 8, 16, 32, 64, 128, 256, …
- z(x)n-1
- z=base
- x=common ratio
- n=sequence number
2
Q
Common Ratio
A
- A ratio of a term to the previous or subsequent term in a geometric sequence
- in {2, 4, 8, 16, 32, 64, 128, 256, …} the common ratio is 2
3
Q
Geometric Series
A
- the sum of a geometric sequence
- 2(3)1-1 + 2(3)2-1+2(3)3-1+2(3)4-1+2(3)5-1
- 2 + 6 + 18 + 54 + 162
4
Q
Function
A
- a function takes one input (x) and generates one specific output (y)
- f(x) = y
- it is NOTa function if there can be multiple outputs for one input
5
Q
Domain
A
- the range of inputs for a function
- the x axis inputs
6
Q
Range
A
- the range of outputs for a function
- the y axis outputs
7
Q
What is the basic Parabola Vertex Formula?
A
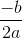
8
Q
Quadratic Equation
A

9
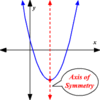
Q
Axis of Symmetry
A
- the line that goes through the vertex of a parabola and that the parabola equally reflects around.
10
Q
Two ways to find the Vertex of a Parabola
A
- create a perfect square from the quadratic
- input an x value so that the perfect square equals zero
- this is the x value of the vertex
- the solution to the equation is the y value of the vertex
Alternate
- if you have the two roots of the parabola…
- take the average of the two roots
- then plug that number into the quadratic equation
- that solution and the average x value equals the vertex
11
Q
What are the Roots of a Function?
A
- points where the x axis is intersected
- these are the point(s) where y is equal to zero
12
Q
How do you find the Roots of a Function?
A
- x2-11x+30
- (x-6)(x-5)
- Roots: x = 6 , x = 5
13
Q
What is the Vertex of a Parabola?
A
- the lowest or highest y value of a parabola
- lowest = positive parabola
- highest = negative parabola
14
Q
What is the Standard Form?
A
- form of an equation with
- variables and coefficients on one side
- constants on the other
- integers only
- ax + by = c
- -14x + 21y = 12
15
Q
How does an exponent operation work?
A
- 32 = 1 * 3 * 3 = 9
- 02 = 1 * 0 * 0 = 0
- 50 = 1
- Also, growth^duration = new/original
- 32 = 9/1 = 9

16
Q
Point-Slope Form
A
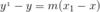
17
Q
Slope-Intercept Form
A
y = mx + b
18
Q
Negative Exponent
A
- invert the base number then perform the exponent operation
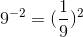
19
Q
Why does exponentation start with 1?
A
- exponentation, and arithmetic in general, is the transformation of numbers
- think of exponentation as starting with a scaling factor, 1 then trasforming it
- start with the scaling factor: 1
- you set the growth factor per interval, x in xn = y
- you set the amount of intervals, n in xn = y
- the answer is the transformed number, y in xn = y
- 34 = 1 (base) * 3 (growth, interval 1) * 3 (interval 2) * 3 (interval 3) * 3 (interval 4) = 81 (transformed number)
20
Q
Why does 00 = 1?
A
- use the microwave analogy
- in 01 think of the microwave as activating the growth factor, in this case 0, so the 0 turns on and obliterates the 1 through multiplication
- however in 00 the growth factor is activated 0 times, it never turns on, so all that’s left is the scaling factor, 1
21
Q
What is a good visual analogy for exponentation?
A
- a tree!

22
Q
How do you factor a quadratic by grouping?
A
- y = Ax2 + Bx + C
- ab = A*C
- a+b = B
- find the factors that satisfy these two equations
- group then factor out terms that make the equations in parenthesis equal
- 4x2+25x-21
- 4 * -21 = -84
- -3 * 28 = -84
- -3 + 28 = 25
- 4x2+28x -3x-21
- 4x(x+7) * -3(x+7)
- (x+7) * (4x-3)
23
Q
What is a rational number?
A
- a number that can be expressed as the ratio of two integers
- 9 = 9/1, 27/3
- 3/2, 7/8
-
decimals that terminate or repeat are rational
- 0.999…
- 0.425425…
24
Q
What are the rules for rational numbers?
A
- the product of a non-zero rational number and an irrational number is irrational: r * i = r
- the reciprocal of an irrational number is irrational: 1/i = i
- the sum of a rational and irrational number is irrational: i + r = i
- the sum or product of two irrational numbers could be rational or irrtational: i + i OR i * i = i OR r
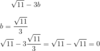
25
How do you factor a quadratic that doesn't share factors?
* find a and b, where **a+b = B and a\*b = A\*C**
* Ex: 8x2-18x-5
* a+b = B = -18
* a\*b = A\*C = -40
* a = 2, b = -20
* Rewrite as **Ax2+ax+bx+C**, and group
* 8x2+2x-20x-5
* (8x2+2x)+(-20x-5) = 2x(4x+1)+-5(4x+1)
* (2x-5)(4x+1)
26
Do both the addition and subtraction rules apply to fractional exponents?
* yes!
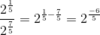
27
What is the equation for the vertext of a parabola from a quadratic?
* y = a(x-h)2 + k
* (h,k) = vertex
* a = coefficient of x2
28
What element of the quadratic tells you whether a parabola opens up or opens down?
* the coefficient of x2
* "a" in ax2+bx+c
* positive "a" opens upwards and negative "-a"opens downwards
29
Explain how the parabola vertex equation works
* y = a(x-h)2 + k
* (h,k) = vertex
* a = coefficient of x2
* if "a" == positive, parabola opens upwards
* if "a" == negative, parabola opens downwards
* if "a" == positive AND x = h
* a(x-h)2 = 0, therefore a(x-h)2 + k = k
* k is the lowest point of y, the vertex
* h is the x value of the vertex
* if "a" == negative AND x = h, k is the highest point of y, the vertex
* a(x-h)2 = 0, therefore a(x-h)2 + k = k
* k is the highest point of y, the vertex
* h is the x value of the vertex
30
Convert a quadratic to the equation of the vertex of a parabola
vertex equation: **y = a(x-h)2+k**
vertex: **(h,k)**
y= 2x2-8x+20
2(x2-4x+10)
2(x2-4x+4)+10-4
2(x-2)2+6
vertex: **(2,6)**
31
How do you solve the for a linear equation to figure out upward or downward shading?
* convert to slope-intercept form: y = mx + b
* 2x + 2y \> 6
* 2y \> -2x + 6
* y \> -x + 3
* so the shaded area is ABOVE the dashed line
32
How do you figure out the amount of solutions for an equality of two equations?
* resolve both sides: 5x-9x+3 = -4x+6-3
* -4x+3 = -4x+3
* 3=3 (infinite solutions)
* solve for x: 10x+7-1 = 5x+4
* 10x-5x=4-6
* 5x=-2
* x=-2/5 (one solution)
* remove constants or variables: 11x-6 = 15x+7-4x
* 11x-6 = 11x+7
* -6=7 (no solutions)
33
How do you find the domain of a function involving a square root?
* it must take the square root of a **non-negative number**
* f(x) = sqrt(2x-8)
* 2x-8 \>= 0
* 2x \>= 8
* x \>= 4
34
How do you find the domain of a function that is a fraction?
* the **denominator** must **not equal** **zero != 0**
* f(x) = (-4-5t)/(1-2t)
* 1-2t != 0
* -2t != -1
* t != 1/2
35
What is a piecewise funcion?
* a function that has different range equations for different number values
36
Give examples illustrating operators and bracket types for piecewise equations.
(-6, 0] = -6 \< x \<= 0
[-1, 22] = -1 \<= x \<= 22
(5, 9) = 5 \< x \< 9
37
What is the form of a perfect square?
(A+B)2 = Ax2+2ABx+B2
38
How do you find and factor a perfect square?
* look for perfect square nomials
* see if they fit the form Ax2+2AB+B2
* if they do then they should equal (A+B)2
39
What is Newton's Formula for finding the square root?
* first give an educated guess at the answer
* then apply the following formula repeatedly to get closer to the actual answer
* **1/2(N / A + A) = New Answer (NA)**
* **1/2(N/NA + NA) = NA**
* **...**
40
What is the absolute value of a number?
* it is the **distance of that number from zero**
* both |-5| and |5| are 5 away from zero
* think of the number line and zero as the mid point
41
How do you interpret an absolute value equation?
* think of it as **how far x is away from the constant**
* ex: in |x-5| = 10 you're asking what numbers are 10 places away from the absolute value of -5 |-5| on the number line
* -5 is 10 away from 5
* 15 is 10 away from 5
* Or get the **absolute value of the answer**: |x-5| = 10 is x-5 = 10 OR x-5 = -10
42
How do you graph an absolute value?
* y = |x+3|
* because the full equation is an absolute value it can't cross the x-axis and will graph as a V on the x-axis
* an equation with a value outside of the absolute value can pass the x-axis: y = |x+3| - 10
43
* an absolute value that **equals zero**
* |x+9| = 0
* x = -9
* any value other than zero will have two solutions
44
How do you solve an absolute value equality?
* get the absolute value on one side and the constants on the other
* eliminate coefficients through division
* solve for the absolute value normally, with the + and - value of the constant
* EXAMPLE
* 2|x+10|+12 = -3|x+10|+62
* 5|x+10| = 50
* |x+10| = 10
* x+10 = +-10
* x = 0, x = -20
45
How do you solve a function that has a square root?
* solve for the square root so that the answer is **greater than or equal to zero: sqrt \>= 0**
46
William is twice as old as Kevin now. 10 years ago William was 7 times as old as Kevin. How old is William now?
* w = 2k
* w-10 = 7(k-10)
* w-10 = 7k-70
* k = 12
* William is now 24 and Kevin is 12. 10 years ago William was 14 and Kevin was 2 (2\*7=14)
47
How do you solve for b in the slope intercept form with two known points? (x,y) (x1,y1)
* y = mx + b
* find the slope using the slope formula m = y-y1/x-x1
* plug the slope into the slope intercept equation along with the x,y of one of the points to find b
* EXAMPLE
* (2,1) (4,2)
* m = (1-2)/(2-4) = -1/-2 = 1/2
* 1 = 1/2(2) + b
* 1 = 1 + b
* b = 0
48
What is the discriminant of the quadratic equation?
* it is the value inside the square root portion of the numerator: **b2-4ac**
49
How do you determine the amount of solutions to a quadratic?
* use **discriminant** of the quadratic equation
* if **b2-4ac \> 0**, then there will be **two solutions**
* if **b2-4ac = 0**, then there will be **one solution**
* if **b2-4ac \< 0**, then there will be **no solutions**
50
How do you determine whether the discriminant of a quadratic is positive, negative or zero by looking at the graph?
* a parabola that **intersects the x-axis at two points** (**two roots**) has a **positive discriminant**
* a parabola that **doesn't the x-axis (no roots)** has a **negative discriminant**
* a parabola that **touches the x-axis at one point** **(repeated root)** has a **zero discriminant**
51
How do you find out if monomials with an integer coefficient (ex. ?4x2y4) is a factor of another?
* divide one by the other, and if you get a monomial with an integer coefficient as the quotient then it is "divisible"
* EXAMPLE
* is 2xy2 a factor of 4x2y4?
* 4x2y4/2xy2 = 2xy2 = YES
52
How do you solve for a function f(v) = u, in terms of v with the following: u-5 = -4(v-1)?
* **solve the equation for u**
* u-5 = -4(v-1)
* u-5 = -4v+4
* u = -4v+4+5
* u = -4v+9
* **-4v + 9**
53
How do you properly convert a word problem to a function formula?
* take the information in the problem and **convert to slope-intercept form**: y = mx + b
* EXAMPLE
* A lake near the Arctic Circle is covered by a 2-meter-thick sheet of ice. In spring the warm air melts the ice and after 3 weeks it's 1.25 meters thick.
* Let S(t) denot the ice sheet's thickness S(measured in meters) and t represent time in weeks.
* S(0) = m(0) + 2
* b = 2
* Two points representing the data points: (0,2) (3, 1.25)
* m = 0.25
* **S(t) = -0.25t + 2** or **S(t) = 2 - 0.25t**
54
In a word problem, what is "rate" equivalent to?
* slope (m); any stated rate essentially tells you the slope
55
What is the easiest way to find b in the point-slope form?
* the y value when x = 0; so in (0, 2.9), b =2.9
56
How do you solve a word problem with a system of equations?
* visualize first as much as possible
* fully analyze the constraints and create equations that fully encompass the two aspects of the question
* find the "lines" and create equations that fully describe them
* include the rates (kilo/h, mph) as factors in the equations and cancel them out
57
What is a system of linear equations?
* two or more linear equations that each have the same unknowns
* it can be solved through substitution, subtraction, graphing, and matrices
58
In what visual ways can you solve a structure word problem?
* visualize the breakdown of each element

59
In what algebraic ways can you solve a structure word problem?
* make the factors equivalent to the amount it is being compared to
* in the problem if c\>d\>d, is b?c+d+b \> 1/3
* b -\> b/3b = 1/3 \> b/c+d+b because b is less than c & d

60
How do you evaluate sequences in recursive form?
* you're evaluating a function that defines a recursive sequence
* you start with a base case and subsequent terms build upon this base case, and in fact require them to find the answer
61
How do you factor polynomials with non-zero leading coefficients?
* complete the square
* find squares in the first and last terms
* EXAMPLE
* 36k2+12k+1
* 36 = 62; 1 = 12
* (6k+1)2
62
What is an arithmetic sequence?
* a sequence where the difference between numbers is always the same, involving addition and subtraction
* EXAMPLES
* {1,5,9,13,17,21,25...} diff = +4
* {28,19,10,1,-8...} diff = -9
* {2,4,8,16,32...} X
* not an arithmetic sequence, as the difference between numbers is different
63
What is the common difference between terms?
* the numerical difference between terms in a sequence
* in {3,9,15,21,27} it is 6
* in {5,-2,-9,-16} it is -7
64
What is a recursive equation for a geometric sequence?
for g(n)
500 if n = 1
**g(n-1) \* 1/5** if n \> 1
65
What is the easiest form of a quadratic to reveal the y-intercept?
* standard form: Ax2+Bx+C
* C = y-intercept
* 3x2+36x+33
* 3(0)2+36(0)+33
* 0+0+33
* 33
66
What form of a quadratic most easily reveals the "zeros" of the equation?
* factored form: a(x-b)(x-c)
* the zeros are the values for x that will make each factor equal zero
* 3(x-3)(x+5)
* zeroes: {3,-5}
67
What is the form of a quadratic that most easily reveals the vertex?
* vertex form: a(x-h)2+k
* vertex= (h,k)
* 2(x-8)+24
* vertex = (8,24)
68
What is the formula for x of the vertex of a parabola from the standard form?
standard form = ax2+bx+c
x = -b/2a
69
What is the best method to use to interpret quadratic models?
* use quadratic forms to find the vertex of the parabolas
* ax2+bx+c -\> a(x-h)+k (h,k)
* The power in watts, P(c)P(c)P, left parenthesis, c, right parenthesis, that is generated by an electrical circuit depends on a current in amperes, ccc, and can be modeled using the function P(c)=-20(c-3)2+180P(c)=−20(c−3)22+180P
70
What is the difference between whole numbers and integers?
* whole numbers are all natural numbers including: 0,1,2,3,4,etc
* integers are all whole numbers and their negative counterparts: -3,-2,-1,0,1,2,3
71
What is another way to define or think about the average rate of change?
* slope
* m = (y1-y2)/(x1-x2)
* slope-intercept form: y = mx+b
* starting value = b

72
* plug in the values to the equation and either
* find the slope
* create a table and find the rate of change from that

73
How do you find the average rate of change from a table?
* simply put the function change over the input change

74
What are the relative minimum and maximum points? How do you express them mathematically?
* the maxiumum and minimum y points on a graph for a particular interval
* they are larger or smaller than the points around them, the peaks or troughs of the graph

75
What are the absolute minimum and maxiumum points?
* the absolute maxiumum and minimum points on a graph over the entire graph
76
What is an exponential function?
* a function where the x value in f(x) is an exponent within the function
* negative exponents are less than 1 and as they grow more negative they get closer to 0 but never exceed it
* after x = 1 the line quickly climbs steeply up the y axis
77
What is the initial value of an exponential function?
* the value before the exponential factor is applied, or 1 \* that value, where x is 0
* in f(x) = 2 \* 5x, the initial value is 2
* f(0) = 2 \* 50 = 2 \* 1 = 2
78
* it is the base of the factor containing the exponent
* in f(x) = 1/5 \* 3x , the common ratio is 3
* this is because 3 is what the exponent factor is being multiplied by, recursively
* f(x) = 1/5 \* 3x
* f(0) = 1/5 \* 30 = 1/5 \* 1
* f(1) = 1/5 \* 31 = 1/5 \* 3 \* h(0)
* f(2) = 1/5 \* 32 = 1/5 \* 3 \* h(1)
* f(3) = 1/5 \* 33 = 1/5 \* 3 \* h(2)

79
What is the form of an exponential equation?
g(x) = a \* r2
80
How do you solve an exponential equation with a graph or series of points?
* treat them like **a system of equations** and **solve using substitution**
* p1 = (0,4) , p2 = (2,8)
* 4 = a \* r0 -
* 4 = a \* 1
* a = 4
* 8 = 2 \* r2
* 4 = r2
* r = 2
* **g(x) = 4 \* 2x**
81
In a g(x) exponential equation how do you solve for x when the common ratio and initial value are given?
* solve like any other equation
* when you get to the exponent x simply convert it to a normal x variable and solve
* you should get some multiple of the common ratio which will tell you what x is
* g(x) = -4
* -4 = -16/49 \* (7/2)x
* 49/4 = (7/2)2
* x = 2
82
What are the best points to find when solving an exponential equation?
* find the **y-intercept** **to easily find a**
* for (0,8)
* 8 = a \* r0
* 8 = a \* 1
* a = 8
* find t**he point where x = 1** **to easily find r** once you have a
* for (1,5)
* 5 = 8 \* r1
* 5/8 = r1
* r = 5/8
83
What is the initial value of an exponential equation on the graph?
* the **y value of the** **y-intercept**
84
How do you solve complex, mult-degree equations?
* first multiply, then factor, then solve
* find at least one x value to solve the equation
* (4x+1)2+9(4x+1) = -18
* multiply then add common factors
* 162+44x+10= -18
* factor the result
* (4x+10)(4x+1) = -18
* find
85
What is the simplest way to solve a quadratic equation where the leading coefficient is != 1?
* factor out the common factor for the whole equation then factor the remainder
* 6x2 - 120x + 600 = 0
* divide by 6
* 6(x2 - 20x + 100) = 0
* 6(x - 10)(x - 10) = 0
* x = 10
86
What is the most elegant way to solve complex quadratics?
* look for **structure and substitute your p's**
* (3x+5)2+5(3x+5)+6=0
* common factor = 3x+5
* **change this common factor into a variable: 3x+5 = p**
* **p2+5p+6 = 0**
* **solve for p**
* **(p+3)(p+2) = 0**
* so **p = -3** OR **p = -2**
* subsitute for p
* **3x+5 = -3 AND 3x+5 = -2**
* **so x = -8/3 OR x = -7/3**
87
What is the simple solution to remember when solving a complex quadratic?
* use the quadratic formula!
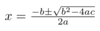
88
How do you solve for r in an exponential equation?
* first take the **ratio of one solution of g(x)** to another
* g(2) = 144
* g(4) = 324
* **144/324 = 9/4**
* then use the **ratio** **to form the equation** **(a\*r4)/(a\*r2)**
* 'a' will cancel out leaving **r4/r2 = r2**
* then make the two solutions equivalent: **r2 = 9/4 = 3/2**
* OR simply **make a table of numbers with x as an integer increasing by 1**. the **common ratio between the y values is r**
* x must be an integer and should increase by 1 to make the division/multiplication operation easier

89
How do you solve for a of an exponential function?
* Method 1: **knowing r and or x, solve for a**
* Method 2: **knowing r, find x = 0 by dividing or multiplying g(x) by r**
* ****x must be an integer and should increase by 1 to make the operation easier
* y of x = 0 is the initial value 'a'

90
How do you use graph values to solve an exponential equation?
* make a **table of values with x as an integer increasing by 1**
* the **ratio of y1 to y2** is the **common ratio r**
* find **x = 0**, and the **y value is the initial value a**

91
92
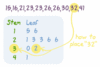
What is a stem and leaf plot?
* a grouping of numerical data where the "stem" is the first part of a value and the "leaves" represent the second part of the value