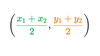Algebra + Coordinate Geometry Flashcards
When are we allowed to subtract inequalities?
We can subtract inequalities in opposite directions
If a > b and d < c, then
a > b
- d < c
= (a-d) > (b-c)
* with the resulting inequality having the same direction as the inequality we subtracted from
When are you allowed to add ineuqalities?
You can add inequalities in the same direction
e.g. If a > b and c > d,
a > b
+ c > d
= (a+c) > (b+d)
If a > b and c > d, then ac > bd - true or false?
False - this may apply to positive numbers, but there is no general rule that applies to multiplication/division of inequalities
even if we multiply big times big and small times small, the inequalities could contain negative numbers, which makes it impossible to predict which of the products would be larger. (e.g. if the two small numbers are negative e.g. -20 and -40 their product would be a large positivie number 400)
x^0 =
1
What happens when you divide or multiply an inequality?
If you multiply or divide both sides of an inequality by a negative number, reverse the direction of the inequality sign (note, if it is positive do not reverse the sign)
2^4 =
16
2^5 =
32
2^6 =
64
2^7 =
128
2^8 =
256
2^9 =
512
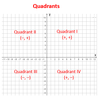
What is the order of the quadrants in the coordinate plane
what is the slope formula?
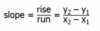
If a line has a slope of 1 or -1, what is the angle it makes with the axes?
45 degress
How do you find the slope of a perpendicular line?
it is the opposite sign reciprocal (swith sign and reverse numerator and denomintor)
What is slope intercept form?
y = mx+b
where:
- m is the slope and
- b is the y intercept
What is the slope of a horizontal line?
What is the slope of a vertical line?
horizontal: 0
vertical: undefined (it is impossible to divide by zero)
What is point slope form?
what is the distance formula?
What is standard form of a quadratic function?
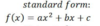
What is vertex form of a quadratic function? Describe all its parts.
In vertex form, if a is negative a quadratic function _____________?
opens downwards
In vertex form, if a is positive a quadratic function _____________?
opens upwards
What is the midpoint formula?
How do you convert a quadratic function from standard form to vertex form? What are the steps?
Complete the square:
- factor ‘a’ out of the first 2 terms
- using the coefficient for the x term, take half that number squared and then add it and subtract it *** best thing to do is subtract it all the way at the end right away so you don’t forget to multiply it by the coefficient
- now the first 3 terms inside the parentheses form a perfect square - factor them
**Note, remember to multiply the 4th term (that isn’t part of the perfect square) that you’re subtracting by the coefficient before taking it out of the parentheses.
- distribute the a value
- collect like terms
E = k
OR
E = -k
What needs to be done before you can solve an abolute value equation?
You need to isolate the absolute value on one side of the equation
How do you solve an aboslute value equation where there is an expression on each side?
What do you need to check for?
- Is always to isolate the absolute value
- Set what is inside the absolute value equal to the other expression and the -1(the other expression)
- Solve
- Check for extraneous solutions (plug into original absolute value equation)
What operations can be performed that preserve a statement of inequality
- You can add the same thing to both sides
- You can subtract the same thing from both sides
(addition and subtraction work exactly the same way for inequalities as they do for regular equations)
What is the rule for multiplying and dividing both sides of an inequality?
You can multiple or divide both sides of an inequality by any positive number, and the inequality will be preserved
BUT
If you multiply or divide both sides by a negative number, you need to switch (flip) the inequality sign to the opposite direction
