AH 2.2.2 Inductance Flashcards
Copy and complete this statement of Faraday’s Law of Electromagnetic Induction.
If a coil of wire is immersed in a ……………………….. magnetic field then a ……………………….. (often called an …………… ) is …………………….. in the coil.
Faraday’s Law of Electromagnetic Induction
If a coil of wire is immersed in a changing magnetic field then a voltage (often called an emf) is induced in the coil.
Copy and complete this statement of Lenz’s Law
The direction of the ………………………. induced in a conductor by a ………………………… magnetic ………………….. is such as to create a field that …………………….. the change causing it.
Lenz’s Law
The direction of current (or voltage) induced in a conductor by a changing magnetic field is such as to create a field that opposes the change causing it.
Look at the situation below involving a coil of wire and a permanent magnet.
a) Is there a reading on the voltmeter?
b) Explain your answer
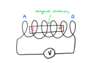
a) There is no reading on the voltmeter
b) As the magnetic is stationary it’s magetic field is unchagning around the coil therefore no voltage is induced
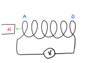
Look at the situation below involving a coil of wire and a permanent magnet.
a) Is there a reading on the voltmeter?
b) Explain your answer
c) Copy the diagram and indicate the magnetic polarity of each end of the coil A and B.
d) Explain your answer to part (c).
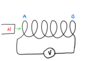
a) Yes, there is a reading on the voltmeter.
b) The magnet is moving so it’s magnetic field moves with it. This constitutes a changing magnetic field around the coil so a voltage (emf) is induced.
c) See the diagram below.
d) Lenz’s Law means that the induced current must flow in such a direction that the magnetic field it creates opposes the change causing it.
As the change causing the induced voltage is an incoming North magnetic pole, then a North pole is etablished at the coil entrance to the coil to oppose it (repulsion). It follows that a South pole must be established at the other end of the coil.
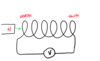
Look at the situation below involving a coil of wire and a permanent magnet.
a) Is there a reading on the voltmeter?
b) Explain your answer
c) Copy the diagram and indicate the magnetic polarity of each end of the coil A and B.
d) Explain your answer to part (c).
a) Yes, there is a reading on the voltmeter.
b) The magnet is moving so it’s magentic field moves with it. This constitutes a changing magnetic field around the coil so a voltage (emf) is induced.
c) See the diagram below.
d) Lenz’s Law means that the induced current must flow in such a direction that the magnetic field it creates opposes the change causing it.
As the change causing the induced voltage is an outgoing North magnetic pole, then a South pole is established at the coil entrance to oppose it (attract the magnet back in). It follows that a North pole must be established at the other end of the coil.

In the circuit shown below the sliding contact S is moved so that the current I increases over time.
a) In which direction (left or right) must the sliding contact be moved to increase the current?
b) Copy the diagram and indicate on it with an arrow above the coil the direction of the induced current.
c) Explain your answer to part (b)

a) to the left
b) see the diagram below
c) According to Lenz’s Law the induced current must act in a direction that opposes the change causing it.
The current causing the change flows anticlockwise (left through the coil) so the induced current must flow clockwise (to the right through the coil).

Copy the circuit shown below and indicate the direction of the induced back emf and give it’s symbol.

As shown below, the back emf is such as to oppose the change causing it. So the back emf opposes the the cell driving the original (changing) current.
Back emf is usually given the symbol ε.
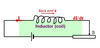
Looking at the circuit below
a) Write down the equation for the induced back emf ε.
b) Name each symbol and give it’s unit.
c) Account for the negative sign in this equation.
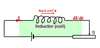
a) ε = -L dI/dt
b) ε = back emf (V)
L = the inductance of the inductor (coil) (Henrys)
I = current (A)
t = time (s)
dI/dt = the rate of change of current (A s-1)
c) The negative sign indicates that the induced back emf opposes the changing current which causes it.
Define the inductance of a coil in words (using the equation as a structure).
Use the back emf equation:
ε = -L dI/dt
The inductance of a coil L is 1 Henry if a changing current dI/dt of 1 Amp per second induces a back emf ε of 1 Volt.
Copy and complete the statement below about how the Law of Conservation of Energy applies to electromagnetic induction:
Work is done by the battery against the ……………. ……………..
This work is ………………….. as energy in the …………………. ………………….
of the inductor.
So energy is ………………………..
Work is done by the battery against the back e.m.f
This work is stored as energy in the magnetic field of the inductor.
So energy is conserved.
In the inductor shown below the current is changing at a rate of 0.4 A s-1 and causes a back emf of 2 V. Find the inductance of the inductor.
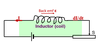
ε = -L dI/dt
-2 = -L x 0.4
L = -2/-0.4
L = 5 H
The circuit below shows an LR circuit (an inductor and resistor in series). The switch is moved to position A, connecting the DC supply to the circuit.
a) Sketch a graph of current v time to show how the current behaves after switch-on.
b) At the moment of switch-on how much voltage is dropped across the resistor?
c) At the moment of switch-on how much voltage is dropped across the inductor?
Let the supply voltage Vs= 6V and the resistor R = 200 Ω.
Ignore the resistance of the coil (which it does have as it is a length of wire but it may be assumed negligible here).
d) Calculate the maximum current that flows and mark it on your graph.
e) What voltage is droppped across the inductor when the current reaches a steady value?

a) See the graph below.
b) 0V. No current is flowing in the circuit so none is flowing in the resistor so it must have 0V across it.
c) 0V. At switch-on no current is flowing in the circuit so none is flowing in the inductor - so it must have 0V across it. This results from the back emf = -Vs at the instant of switch on. At this instant the back emf effectively balances the supply voltage leaving a net voltage of 0V across the inductor.
d) I = 0 at swich-on as this is when dI/dt is maximum and the back emf ε = -L dI/dt
As dI/dt decreases so ε decreases therfore I increases, as shown in the graph below.
The maximum value of I is when I is steady and is found by applying Ohm’s Law to the resistor thus
Imax = Vs/R = 6/200 = 0.03 A
e) When I reaches a steady value it is clearly not changing, so dI/dt = 0. This means ε = -L dI/dt = 0 i.e. the inductor provides NO back emf. In effect the inductor at this stage acts simply as a length of conducting wire (assumed to be of negligible resistance here).
So no voltage is dropped across the coil and all of the supply voltage is dropped across the resistor

In the circuit below, current has been flowing for some time and has reached it’s maxium steady-state value.
a) What is the value of the back emf ε in the inductor?
b) The supply has done work in overcoming the back emf of the inductor. Where has the energy fom the supply gone?
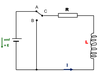
a) 0A
b) Energy is stored in the magnetic field of the inductor.
(We are ignoring resistive heating of the wire of the inductor).
What is the equation for the energy stored in an inductor when supplied with current?
Name each symbol and give it’s unit.
W = 1/2 LI2
W = energy stored in inductor (J).
L = Inductance of inductor (H)
I = maximum current flowing inductor (A).
A 0.500 H inductor is connected to a 10.0 V DC supply in series with a 500 Ω resistor.
a) Find the maximum value of the current after it reaches a steady value.
b) Energy is stored in the inductor. Describe how this is possible.
c) Find the amount of energy stored in the inductor.
The supply is now switched off.
d) What happens to the magnetic field of the inductor?
e) What happens to the energy previously stored in the inductor?
a) Imax = Vs/R = 10.0 / 500 = 0.0200 A
b) Energy is stored in the magnetic field of the inductor.
c) W = 1/2 LI2
= 1/2 x 0.500 x (0.0200)2
W = 0.0001 J
d) When the current is switched off the magnetic field collapses and reduces to zero.
e) The energy stored in the inductor is returned to the circuit as a back emf which opposes the collapse.
In an AC circuit with an inductor:
a) What is meant by Inductive Reactance XL. (Answer in words).
Specify it’s unit.
b) State the relationship between RMS current IRMS in an inductve circuit and the frequency f of the AC supply.
c) Sketch a graph of RMS current through an inductor and the frequency of the AC supply. Assume the voltage from the supply is contant at all frequencies.
a) Inductive Reactance XL is the opposition of an inductor to current flow (Ω).
b) XC α 1/ f
c) See the graph below.

a) For an AC circuit, state the equation relating inductive reactance XL to the voltage across the inductor V and the RMS current through the inductor IRMS.
b) State the equation for XL in terms of frequency
c) Combine the two equations above to find an expression for the RMS current in an inductive circuit.
a) XL = V/IRMS
b) XL = 2πfL
c) XL = V/IRMS
2πfL = V/IRMS
IRMS = V / 2πfL
Given that, in AC circuits
XL = 2πfL so XLα f L = constant
XC = 1/2πfC so XC α 1/ f C = constant
Sketch on one set of axes the relationship between
XL and f as well as XC and f

Comparing inductors and capacitors in AC circuits,
a) Which opposes high frequency signals more?
b) Which opposes low-frequency signals more?
c) Which effectively blocks DC signals?
a) Inductors oppose high frequency signals more
b) Capacitors oppose low frequency signals more
c) Capacitors effectively block DC (although there is a short burst of current during the initial charging phase, but this is short-lived).
See the graph below.

One very common application of capacitors and inductors together is in the cross-over networks of hi-fi speakers.
The diagram below shows a two-way cross-over network feeding two loudspeakers called a ‘tweeter’ and a ‘woofer’.
There is a high-pass filter in the tweeter circuit and a low-pass filter in the woofer circuit.
a) What is meant by ‘high-pass filter’ and ‘low-pass filter’?
b) Explain how these filters work by referring to the reactance equations.
c) Why this is desirable in a high quality loudspeaker?

a) A high-pass filter allows high frequency AC signals past but opposes low frequency signals.
A low-pass filter allows low frequency AC signals past but opposes high frequency signals.
b) The capacitor in the high-pass filter of the tweeter circuit has reactance XC = 1/2πfC. So it has a high opposition to low frequencies and so the low frequency signals’ current is very small. The tweeter therfore receives only high frequency signals.
The inductor in the low-pass filter of the woofer circuit has reactance XC = 2πfL. So it has a high opposition to high frequencies and so the high frequency signals’ current is very small. The woofer therefore receives only low frequency signals.
c) Tweeters are very small in order to move at the very high frequencies required of them. They are unable to reproduce low frequencies and could be damaged if a low frequency signal of sufficient amplitude were supplied to them.
Woofers are very large because they produce low frequencies of sound which therfore have larger wavelengths. This means they must move a much larger volume of air in operation than tweeters. If a woofer is supplied with a high frequency signal it cannot move enough air to cool itself and so can over heat and be damaged.


