AH 1.5 General Relativity Flashcards
In the spacetime diagram below, the blue shaded region is called time like.
What do the world lines on this diagram represent?
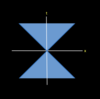
Light, travelling at 3 x 108 ms-1.
What is meant by inertial mass ?
Inertial mass measures a body’s resistance to being accelerated (i.e. have its momentum changed) and is the ‘m’ in mv = momentum.
Notice that inertial mass makes no reference to gravity.
What is the relationship between gravitational mass and inertial mass ?
Inertial and gravitational mass are equivalent
Explain what is meant by the equivalence principle.
The Equivalence Principle (EP) states that inertial mass is equal to gravitational mass. Or, put another way, there is no experiment that will discern the difference between the effect of gravity and the effect of acceleration.
Einstein used the equivalence principle to show that the path of a ray of ligth woud be affected by what?
Einstein used the equivalence principle to show that the path of a ray of ligth woud be affected by gravity.
Copy and complete this statement:
Einstein used the equivalence principle to show that the stronger the ……………………. …………………………. the more ……………………. a clock would run.
Einstein used the equivalence principle to show that the stronger the gravitational field the more slowly a clock would run.
Which clock runs mores slowly - one at sea level or one at the top of Ben Nevis? Explain your answer.
The clock at sea level runs more slowly.
This is because it is closer to the Earth’s centre (i.e. at lower altitude) and so is in a stronger gravitational field.
The stronger the gravitational field, the more slowly a clock runs.
Look at the spacetime diagram below and identify the motions of each line (a), (b) and (c).
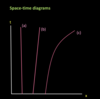
(a) stationary
(b) uniform speed
(c) iniform acceleration
What are the lines drawn on a spacetime diagram called?
World lines (or geodesics).
Copy and complete the following statement.
Euclidean space has co-ordinates which uniquely specify a point in space – a location.
Spacetime locates not points in space but ………………………… i.e. not just ……………………… something happens but also ……………………..
Spacetime locates not points in space but events i.e. not just where something happens but also when.
How can gravity be explained ith refrenece to spacetime?
The presence of a massive object, like the earth, curves the ‘fabric’ of space-time. So gravity warps spacetime, as shown below.

By referring to spacetime, explain what is happening in the diagram of the Earth and the Sun below.

The Earth follows the curvature of the spacetime which has been curved by the mass of the sun.
Look at the diagram below.
Explain what is going on.

General Relativity suggests that photons are affected by gravity, meaning that light from distant stars is bent as it passes a massive object like the sun.
This results in the apparent (observed) position of the star being different form its actual position in the sky.
With the aid of a diagram, explain how gravitational lensing occurs.
Massive cosmic objects, such as a galaxy bend and focus the light that flows around them using their gravity, acting like giant magnifying glasses. This effect is called gravitational lensing.
The diagram below shows the effect.

Describe in words what is meant by a black hole.
A black hole is a star of such high density that it’s escape velocity is greater than the speed of light. So, not even light can escape it’s gravitational pull.
Starting with the density equation ρ = m / V, show that, for any spherical star mass m, radius r
m /r = 4/3 ρ π r2
Note that this is not a required derivation, but you should be able to do it!
ρ = m / V
ρ = m / 4/3 π r3
ρ = m / (r x 4/3 π r2)
m /r = 4/3 ρ π r2
Given that the escape velocity may be given by
vesc = √ (8Gπr2ρ/3)
…find the escape velocity from a star which has
mass = 8.2×1036 kg
radius = 1.230 x 1010 m
volume 7.795 x 1030 m3
Is this star a black hole?
The stellar density is
ρ = m/V = 8.2×1036 / 7.795 x 1030 = 1.05195 x 106 kg m-3
vesc = √ (8Gπr2ρ/3)
vesc = 5.17 x 108 ms-1
As vesc > c then this is indeed a black hole.
Name ‘A’ and ‘B’ in the diagram below.

A singularity
B event horizon
Insert ther missing words.
An object far enough above the surface of a the singularity feels a …………………… gravitational pull than on its surface – so the escape velocity is …………………. up there.
At a certain (big enough) radius the escape velocity drops to ………. …………. ….. ……………………..
At or beyond this level light can ……………………… from the black hole.
This boundary is called the ……………… …………………
An object far enough above the surface of a the singularity feels a weaker gravitational pull than on its surface – so the escape velocity is smaller up there.
At a certain (big enough) radius the escape velocity drops to the speed of light.
At or beyond this level light can escape from the black hole.
This boundary is called the event horizon.
Explain what is meant by the event horizon of a black hole.
The event horizon is the boundary defining the region of space around a black hole from which nothing, not even light can escape, as shown in the diagram below.

Look at the diagram of a black hole below.
a) Would light originiating at point X escape from the black hole? Explain your answer.
b) Would light originiating at point Y escape from the black hole? Explain your answer.

a) No. This light is closer to the singularity than the event horizon. The gravitational field is so strong here not even light can escape.
b) Yes. This light is further from the singularity than the event horizon. The gravitational field is less strong here and light can escape.
With the aid of a diagram, explain what happens to the passage of time as one approaches a black hole.
Time runs more slowly as one approaches a black hole.
Explanation:
Gravity curves spacetime.
So, whereas light would travel in a straight line in the absence of a gravitaitonal field ( a —> b below), it travels in a curved path when there is a gravitatonal field (c —> d below).
Light travels at a constant speed so must take longer to travel from c to d than from a to b.
So time runs slower wherever gravity is strongest, because gravity curves space-time.
This is gravitational time dilation

a) Name rs in the equation below.
rs = 2Gm/c2
b) Explain what rs is.
a) rs = the Schwarzschild radius.
b) The Schwarzschild radius (rs) is the radius of the event horizon surrounding a (non-rotating) black hole, as shown in the diagram below.

Calculate the Schwarzchild Radius rs of a star of mass
2.8 × 1030 kg
(rs = 2Gm/c2)
rs = 4.2 × 103 m



