AH 1.4 Gravitation

Question 1

What is meant by a gravitational field?

Answer 1

A gravitational field is the region in space within which a small test mass would feel the gravitational force of a planet (or other massive body).

Question 2

Define the gravitational field strength of a massive body.

Answer 2

The gravitational field strength of a body is the gravitational force exerted by that body on a 1 kg test mass.

Question 3

Sketch the gravitational field lines for an isolated point mass.

Answer 3

Question 4

Sketch gravitational field lines around two adjacent point masses.

Answer 4

Question 5

State in words what is meant by the gravitational potential at a point in a gravitational field.

Answer 5

The gravitational potential at a point in a gravitational field is

the work done by an external force in bringing a unit mass from infinity to

that point

Question 6

Where is the zero of gravitational potential taken to be?

Answer 6

The zero of gravitational potential is taken to be at infinity.

Question 7

State the equation which describes Newton’s Universal Law of Gravitation, which gives the expression for the force of attraction, F, between the two masses shown in the diagram below.

Answer 7

Question 8

Calculate the force of attraction between Martin, mass 50 kg and Joseph, mass 55 kg if they sit 50 cm apart. Comment on the size of the force.

Answer 8

Question 10

The Earth has a radius of 6.38 × 10⁶ m and a mass 5.97 × 10²⁴ kg. What is the gravitational force due to the Earth acting on a woman of mass 60.0 kg standing on the surface of the Earth?

Answer 10

Question 11

By equating the weight equation W=mg with Newton’s Universal Law of Gravitation, show that the gravitational field strength of the Earth’s surface g, is given by

g = Gm/r²

where m= mass of the Earth and r = radius of the Earth

Answer 11

Question 12

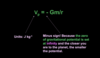
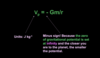
For a planet, state the equation for the gravitational potential V_p at a point in it’s gravitational field a distance r from it’s centre. Specify the units of gravitational potential.

Answer 12

Question 13

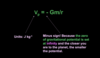
V_p = -Gm/r

What does V_p stand for?

What is it’s unit?

What is the significance of the minus sign?

Answer 13

V_p = gravitational potential

It is masured in J kg^-1

The zero of gravitational potential is set at infinity and

the closer you are to the planet, the smaller the gravitational potential.

These two factors mean gravitational potential is always negative.

Question 14

Gravitational potential a property of what?

Answer 14

Gravitational potential a property of the field.

Question 15

Must a test mass exist for the gravitational potential of a planet to exist?

Answer 15

No. Gravitational potential is a property of the field itself.

(It is called ‘potential’ because if a test mass WERE brought into the field, then work WOULD have to be done by the field to bring it there form infinity).

Question 16

Given that gravitational potential is given by V_p= -Gm/r, sketch a graph of V_p against r around the earth, where r is the distance from the centre of the Earth and m is the mass of the Earth.

Answer 16

Question 17

Complete the following sentence:

Gravitational Potential Energy is the gravitational potential per …

Answer 17

Gravitational Potential Energy is the gravitational potential per unit mass.

Question 18

Given tha Gravitational Potential Energy is the gravitational potential per unit mass and that V_p=-Gm₁/r, state the equation for the gravitational potential energy E_p of a mass m₂ placed in the gravtiational field a distance r from the centre of a planet mass m₁

Answer 18

E_p = V_p x m₂ = - G m₁ m₂ / r

Question 19

With the aid of a diagram, explain what is meant by a conservative field.

Answer 19

Question 20

State in words what is meant by escape velocity.

Answer 20

The escape velocity for a given planet is the minimum velocity a body must achieve in order to completely escape the planet’s gravitational field and so reach infinity.

Question 21

Derive the expression for escape velocity of a rocket from the surface of the Earth given below.

Answer 21

Work Done by rocket = E_p (at infinity) - E_p (on Earth’s surface)

» ΔEp = -GmEm / ∞ - (-GmEm / rE)

» ΔEp = 0 - (-GmEm / rE)

» ΔEp = GmEm / rE

= the minimum kinetic energy rocket must have to escape

So ½ mv² = Gm_Em / r_E

v² = 2Gm_E / r_E

v = √ 2Gm_E / r_E

Question 22

Identify the cause of the centripetal force which makes this satellite to describe uniform circular motion around the Earth, as shown below.

Give the equation for this force F, taking the mass of the Earth as m_E, that of the satellite as m and the distance between the centre of the Earth and the satellite as r.

Answer 22

The gravitational attraction of the Earth for the satellite.

F = GM_Em/r²

Question 23

Find and expression for the linear speed v of a satellite orbitting the Earth by equating the gravitational force on the satellite

F = G m_Em/r²

and the centripeatl force

F = mv²/r

Where

m = mass of satellite

M_E = mass of Earth

r = distance between centre of Earth and satellite

Answer 23

G m_Em/r² = mv²/r

v² = G m_E/r

v = √G m_E/r

Question 24

Beginning with the linear speed equation v = d / t , find an expression for the orbital period T of a satellite orbitting the Earth.

Answer 24

v = d / t = 2πr / T

2πr / T = √G m_E/r

T / 2πr = √ (r / G m_E )

T = 2π √r₂ x √ r / G m_E

T = 2π √r³ / G m_E