A refresher on math Flashcards
(38 cards)
Vector space definition
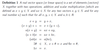
Distance

Normed vector space

Limit of a sequence

Limit point

Limit points of a convergent sequence
A convergent sequence in R_n can have at most one limit point
Theorem 3 Convergence and boundedness
Every convergent subsequence in R_n is bounded
Definition Cauchy sequence

Theorem 5 convergence of cauchy sequences
Every cauchy sequence in a metric space
- The sequence is bounded
- The sequence has at most one limit point
Def complete space
Every Cauchy sequence is convergent (to a point within the metric space)
Continuity of a mapping at a point

Pointwise convergence
Notice pointwise convergence doesn’t preserve continuity
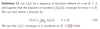
Uniform convergence

Theorem 5 uniform convergence

Uniform convergence theorem

C(X)

Def contraction mapping

Banach fixed point theorem

Corollary Banach

Blackwell’s sufficiency conditions

Definition correspondence

Definitions of correspondence:
- compact valued
- closed valued
- convex valued
Their images are respectively:
- compact sets
- closed sets
- convex sets
Graph of a correspondence
Analogously, we have:
- Closed-graph correspondences
- Convex-graph correspondences

Lower hemi-continuous
lhc fails if there are discontinuities that blow up the “upper border” of the graph














