3a Scatterplots and Regression Flashcards
(13 cards)
Interpreting Correlation
Correlation is just r. Gives direction and strength. r = 0.7 means there is a strong positive relationship between these variables. NOTE: r should only be used when the data is roughly linear but just knowing r (even if it is high) doesn’t guarantee linearity.
Explanatory Variable
x, input, independent variable. Usually, this is what is changed. In an experiment, the treatments are the explanatory. Ex. rubber bands explain distance traveled.
Response Variable
y, output, dependent. This is usually what is measured as a result of changes in the explanatory. Ex. We added rubber bands and measured the distance traveled (response variable)
Describe a relationship or scatterplot
DUFS (direction, unusual points, form, strength). Usually in one sentence: There is a strong, positive, linear relationship…
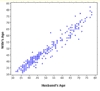
Scatterplot
Each dot represents 2 variables for one individual. In this graph, the “individuals” are married couples.
Positive Association
As x increases, y increases
As x decreases, y decreases
Positive correlation

Negative Association
As x increases, y decreases
As x decreases, y increases
Negative correlation
What is Correlation?
“r”
Always between -1 and 1.
As r-value becomes closer to 1 (or -1, the correlation becomes stronger

How do you find and interpret a residual?
Actual minus predicted OR observed - expected (y-ŷ)
To get the predicted, you plug the x-value into the LSRL. They have to give you the actual value.
Interpretation: The actual (y-context) for this (specific x-value) was (residual) more/less than predicted.
Ex. The actual distance traveled for Barbie with 5 rubber bands was 1.47 in. more than predicted.
How do you find and interpret the slope of the LSRL?
“b” value in ŷ=a+bx.
Interpret the slope:
For each additional (x-context) the predicted (y-context) (increases/decreases) by (slope).
“For each additional mile driven, the predicted sales price of a truck decreases by $15.” OR “We predict that the sales price of a truck will lose $15 for each additional mile driven.”
How do you find and interpret the y-intercept of the LSRL?
“a” value in ŷ=a+bx
Interpret the y-intercept:
When (x=0 context) the predicted (y-context) is (y-int).
“A truck with 0 miles on it is predicted to sell for $45,000”
What is a residual plot?
A plot representing the x values and residual values (y-ŷ).
It’s like you just take the LSRL and make it horizontal and zoom in a little on all of the differences.
How do you tell if a linear model is appropriate?
If given a residual plot: if there’s no pattern in the residual (a curve or all the points on one side are positive but generally negative on the other side) a liner model is appropriate. If there is a clear pattern in the residual plot, a linear model is not appropriate.


