2 OLS (Ordinary Least Squares)

Question 1

What are econometrics used for?

Answer 1

1. Estimating economic relationships
2. Testing economic theories
3. Evaluating policies

Question 2

Which procedures are not experimental?

Answer 2

1. Cross section
2. Pooled cross section
3. Time series
4. Panel data

Question 3

What is the question of linear regression?

Answer 3

Understanding how y (DV) varies with x (IV).

Question 4

What is the typical form of a linear regression model?

Answer 4

y = β₀ + β₁x + u

We wanna estimate β₀ & β₁

u is the error term, E(u) = 0

Question 5

What is the zero conditional mean assumption?

Answer 5

E(u⎪x) = E(u) = 0

The estimate value doesn’t depend on the value of x.

Thus, the estimator is unbiased.

Question 6

How do you compute β₁ & β₂?

Answer 6

Question 7

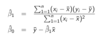
What is th criteria to choose β₁ & β₂?

Answer 7

They must minimize the sum of squared residuals

(û_i = y_i - ŷ_i)

Question 8

What is a residual?

Answer 8

The difference between reality and the fitted value found with the regression equation.

Question 9

What are the 3 mechanical properties of the OLS?

Answer 9

1. Σû_i = 0
2. cov (û, x) = 0
3. point (Ẋ, ȳ) always on the regression line

The residual is not correlated with x.

​​

Question 10

When is the OLS unbiased?

4 conditions.

Answer 10

1. Linearity in parameters.
2. Random sample
3. Zero conditional mean
4. Sample variation in the regressor (no variation of x)

Question 11

β^₁ = Δŷ/Δx is equivalent to…

Answer 11

Δŷ = β^₁Δx

Question 12

If the zero conditional mean assumption fails, what could we obtain?

Answer 12

A “spurious correlation”. There is a mistake in the data collection, so the result can’t be right.

Question 13

Which ratio does measure the quality of the model?

How is it computed?

Answer 13

R²

We need to handle this information with care.

Question 14

What are the different types of model we can have for a regression?

Answer 14

• Linear
• Quadratic
• Natural logarithms ( y = log (x) )

For non-linear models, Δŷ depends on the initial value of x.

Question 15

What is a logarithm?

Answer 15

The log of a number is the exponent by which another fixed value, the base, has to be raised to produce that number.

ex: log₁₀(1000) = 3

1000 = 10³

More generally: x = b^y < = > y = log_b(x)

Question 16

For very small changes in x, how can we compute the change in log?

Answer 16

Δlog(x) = log(x₁) - log(x₀) ≈ (x₁-x₀)/x₀ = Δx/x₀

100Δlog(x) ≈ 100Δx/x₀ = %Δx

This is true only for small changes!

Question 17

For a linear regression, how do you compute an elasticity?

Answer 17