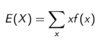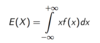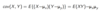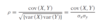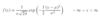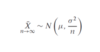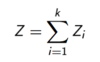1 Probability and random variable Flashcards
What is an experiment?
Procedure that can be repeated many times and has a well defines set of outcomes.
How do you write the probability for the event A?
P(A)
What does means “P(A)”?
Proportion of times the event A will occur in repeated trials of an experiment.
For a large number of trials, a relative frequence will provide a good approximation of the probability of A.
What is a “function”?
Relation between a set of input & a set of possible outputs, with the property that each input is related to exactly ONE output.
What are the properties for a P(A), a real-valued function?
Function defigned in R.
0≤P(A)≤1
If A, B, C ….. constitute an exhaustive set of events, P(A+B+C+…) = 1 where A+B+C means A or B, or C and so forth
If A, B, C … are mutually exclusive events,
P(A+B+C+…) = P(A)+P(B)+P(C)+…
What is a random variable?
Numerical variable whose value is determined by the outcome of a random experience.
This value is unknown until observed.
What type can be a random variable?
Discrete: take only a finite number of values
Continuous: it ca take on any value in some interval of values & take on any particular value with a zero probability, because there is so many possibilities. Each one has a probility of 0 to happen, statistically.
How is a random variable denoted?
X, Y, Z…
Its values are {x, y, z…}
What does indicate a discrete probability density function?
P(X=xi) indicates the probability that the discrete random variable X takes the value xi.
How do you write the discrete PDF?
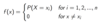
For a continuous function, what is the propability for a specific value?
0
For a continuous variable, how do you determine the probability of an event?
You must take an interval and calculate the probability of getting this event as the outcome.
How do you write the continuous PDF?
Where P(a
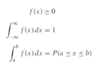
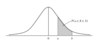
What is an integral for a continuous PDF?
The area under the PDF between the points a and b.
What is a cumulative distribution function (CDF)?
It is a sum of all the probabilities between the minimum and xi.
What is the formula of the CDF?
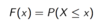
Properties of the CDF, for all important continuous distributions:
- P(X>c) = ?
- P(X>c) = ?
- P(X< -c) = ?
- For any a < b, P(a < X ≤ b) = ?
- P(X>c) = P(X≥c)
- P(X>c) = 1-F(c)
- P(X< -c) = P(X>c) if symmetric
- For any a < b, P(a < X ≤ b) = F(b) - F(a)
What is a Discrete Joint PDF?
Probability observ outcome x of X and y of Y at the same time.
How do you compute teh Discrete Marginal PDF?
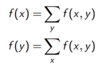
What is a conditional PDF?
Probability that X takes the value x given that Y has assumed the value y.
What is the formula for a Conditional PDF?
When are 2 random variables statistically independent?
If the joint PDF can be expressed as the product of the marginal PDFs for all combinations of X and Y.
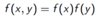
If X and Y are independent, then, f(x⎪y) = ?
f(x⎪y) = f(x)
y doesn’t convey any information on x’s distribution.
WHat is an expected value?
It is the (population) mean of the distribution.
What is the formula for the expected value for a discrete distribution?
What is the formlula of the expected value for a continuous distribution?
Properties of the expected value:
- If a is constant, E(a) = ?
- if a & b are constant, E(aX + b) = ?
- For 2 rv X &Y, E(X, Y) = ?
- For a function g(.), E[g(x)] = ?
- If X & Y are 2 independent variables, E(XY) = ?
- If a is constant, E(a) =a
- if a & b are constant, E(aX + b) = aE(X) + b
- For 2 rv X &Y, E(X, Y) = E(X) + E(Y)
- For a function g(.), E[g(x)] = Σxg(x)f(x)
- If X & Y are 2 indep var, E(XY) = E(X)E(Y)
What is a Median m?
It measures the central tendency of a distribution.
- Continuous: value such that 1/2 of the area under the PDF is set at the left of m and 1/2 is at the right of m.
- Discrete
- X takes on a finite numer of odd values: order the values of X and select the one in the middle.
- X takes on a even number of values: average the 2 middle ones.
If the distribution is not symmetric around the mean, what happen to the expected value and the median?
The differ.
What is the variance?
It is the expected distance from the mean.
What is the formula of the variance?
E(X)=μ
var(X) = E(X)²- [E(X)]²
Or
What are the other formulas of the variance?
Is E[g(x)] = g[E(x)]?
NO!!!!!!
It is a non-linear function.
Properties of the variance:
What is covariance?
It measures the amount of linear dependence between 2 rvs.
What is the formula for covariance?
If X & Y are discrete, what is the formula for the covariance?
Properties of covariance?
What is a correlation?
What is its particularty compared to covariance?
Correlation (ρ) is a measure of the linear association between 2 variables.
The correlation doesn’t depend on the unit of measurement, whereas covariance does.
What are the max (& min) values of ρ?
What are their meanings?
+1 and -1
- +1: perfect positive association.
- -1: perfect negative association.
What is the formula of the correlation?
Variance of correlated variables:
var(X +Y)= ?
var(X −Y)= ?
var (X+Y) = var(X)+var(Y)+2cov(X,Y)
var(X −Y)=var(X)+var(Y)−2cov(X,Y)
If independence, the thirs term drops.
Why do we use the Z transformation?
It indicates the number of time the observation is far away from the mean in σ.
How do you compute a Z score?
Z = (x-μ)/σx
σ²z = ?
σ²z = 1
What is the Conditional expectation of Y given X?
It is a weighted average of possible values of Y, but the weights reflect the fact tha X has taken on a specific value.
What is the PDF of a rv said to be normally distributed?
How is denoted a normally distributed rv?
X ∼N(μ, σ²)
What are the 2 properties of a normally distributed rv?
- It is symmetrical around the mean
- It only deepends on μ and σ²
How is represented a normally distributed rv?
How is represented the CDF of a normallt distributed rv?
What are the mean and the unit for a Z score?
Mean: 0
Unit: σ
What is the central limit theorem?
This kind of distribution is always normal.
What is the Chi2
It is a distribution based on the sum of random variables distributed normally.
Z posses the Chi2 distribution with k degree of freedom (df).
What is a Student’s distribution?
What is inference?
It is a process that allows us to learn something about a population given the availability of a random sample from that population.
What are the steps of the inference?
- Identify a relevant population
- Draw a sample
- Specify a model
- Estimate (point or interval) & hypothesis testing
What is a random sample?
Subset of individuals chosen from a population such that:
- Each individual is chosen randomly and entierly by chance.
- Each subset of k individuals has the same chance to be chosen.
- It can be done with or without replacement (n → ∞).
What are the main analyses we can compute on a sample?
- Mean / sample average
- Sample variance (that follows a Chi2 distribution).
- Sample covariance.
What is an estimator?
Rule assigning to an unknown parameter of the underlying population distribution a unique value for each possible sample realization.
We can have plenty of different estimators for the same unknown paramter, each one is a rv.
How do you choose the right estimator?
Look at the sampling distribution.
When is an indicator unbiased?
When: E(W)=θ
Maybe the estimator is far from the parameter, but if we do infinite times, it is fine.
What is a confidence interval?
Computing the smallest interval possible in which θ has the major probability to be.
θ is the value for the population, so we don’t know it.
What happen to a confidence interval when then sample is bigger and bigger?
It becomes smaller and smaller.
When is an estimator consistent?
When the distribution of this estimator becomes more and more concentrated near the true value of the paramter being estimated.
