Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

A2 Physics Knowledge > §11 THERMAL PHYSICS Knowledge > Flashcards

§11 THERMAL PHYSICS Knowledge Flashcards

1
Q

What two processes can cause energy transfer between two objects.

A
  1. Heat transfer to/from object
  2. Work done on/by object.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is ‘heat transfer’, ΔQ

A
  • Heat transfer is energy transfer due to a temperature difference.
  • Heat energy moves from a higher T region to a lower T region.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What is mechanical ‘work’; can you give an example of how it produces a change in U?, ΔW

A
  • Is an energy transfer process where there is no transfer of heat, i.e. internal energy is changed by doing mechanical work,
  • Work is the name given to the energy transferred when a force is applied across a distance • Work is done and there is a rise in temperature due to an increase in internal energy (remember however that no heat transfer has taken place).
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What is the ‘direction’ of heat transfer under ordinary circumstances.

A

• Heat transfer takes place from the hotter object to the colder object.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

What are the 3 types of heat transfer process?

A

• (1 )Radiation • (2) Convection • (3) Conduction • Can occur either to/from an object.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What is ‘internal energy’?

A

The internal energy of an object, is the sum of the random distribution of the kinetic and potential energies of its molecules.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

How is internal energy related to the microscopic structure of a substance?

A

U [internal energy] is the energy of an object due to the constituent particles’: • Individual positions (potential energy) • Motion (kinetic energy)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

What is ‘thermal energy’?

A

• Thermal energy: the internal energy of an object due to its temperature.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

What’s the difference between ‘internal energy’ and ‘thermal energy’

A

• Internal energy U may not equal the object’s thermal energy, • ∵ Some of the U may be from sources other than thermal ones.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Can you give an example of part of an object’s internal energy not coming from a ‘thermal’ source?

A

• A magnetic Fe bar has greater U when magnetised then when demagnetised. • This is U but not due to an object’s temperature.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Can you give an example of work done ON an object?

A

• Stirring a teacup very vigorously can increase its internal energy (• This is more than offset by convection resulting in heat transfer out of the cup)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

What do you know if ΔU = 0 (so U is constant)?

A

(1LT) ΔU = ΔQ + ΔW • If ΔU = 0, ΔQ = - ΔW • So (1) no heat transfer/work done to/from/on/by the object. OR (2) Thermal equilibrium (3) Work done on object = heat energy lost by object. (Isothermal)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What is thermal equilibrium

A

• No overall transfer of heat… • … between two objects of the same temperature.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Why do the brake pads of a braking car gain U?

A

• Moving vehicle has KE • Friction does work on BP when pressed. • KE → ΔW → U increase • Higher U manifest as higher temperature of the brake pad

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

How could ΔU = 0 for a filament in a running filament bulb?

A

• FB turned on → Elec. supply does ΔW in pushing electrons through high resistance filament. • ΔW on filament ΔU = ΔW, U increases. • ∴ Filament temperature increases to operating temp. • At O.T. negative ΔQ: heat transferred to surroundings (temp-diff) and light is radiated. • … Until ΔW = – ΔQ → ΔU = 0 • ∴Constant internal energy of lightbulb filament.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Give 4 examples of how doing mechanical work on an object changes its internal energy

A

• Work done by electricity e.g. on a filament bulb • banging your head on a table • hitting a golf ball with a club etc. • An important example of changing internal energy by doing work is the compression or expansion of a gas (compression - work done ON gas , expansion - work done BY gas)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

What is the definition of ‘temperature’

A

• A measure of the average internal energy an object has. • In simple terms, ‘the degree of hotness of an object’.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

What is the ‘specific latent heat of fusion’

A

The specific latent heat of fusion is: • the energy needed to change 1 kg of the substance from solid to liquid… • … when the solid is at its melting point (at constant temperature). • Unit of SLHF = J/kg

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

What’s an expression for the energy required to change (m) kg of solid to liquid at constant temperature (m.p.)

A

• Q = m x SPECIFIC latent heat of fusion

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

What is the ‘specific latent heat of vaporisation’

A

The specific latent heat of vaporisation is: • the energy required to turn unit mass (1 kg) of the substance from liquid state to vapour, • without causing a change of temperature (at its b.p.) Unit : J / kg - Once again, when boiling point is reached, the energy supplied does not change temperature but is used to free molecules from the liquid to become gas (or vapour).

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

What’s an expression for the energy required to change (m) g of gas to a liquid at constant temperature?

A

• Q = m x Specific latent heat of Vaporisation

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

When the latent heat of vaporisation is supplied to a liquid at its boiling point, where does the energy go?

A

• When boiling point is reached….(or when the liquid evaporates in general) • … the energy supplied does not change temperature…. • … but is used to free molecules from the liquid, to change the phase to gas (or vapour).

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

What are the 4 phases of matter

A
  1. Solid, 2. Liquid. 3. Gas 4. Plasma - but only at v.high temperatures (e.g. fusion reactors or stars) so not in spec.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

What’s the difference between the terms ‘state of matter’ and ‘phase of matter’?

A
  • Phase of matter ≠ state of matter necessarily • Phase : Solid / liquid / gas
  • State of a system can be changed by changing temperature, pressure or volume
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

What does this show?

A
  • The gradients of the solid, liquid and gas are not necessarily the same.
  • The time axis is directly proportional to an energy axis because W = Pt, the constant of proportionality is the power.
  • The time D to E is greater than that of B to C because the latent heat of vaporisation is greater than the latent heat of fusion.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

What assumptions are made in the experiment used to draw this graph?

A

Assuming:

  1. No heat loss occurs during the heating phase
  2. That energy is supplied at a constant rate P to that substance
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

Look between A and B

  • What is the physical meaning of the gradient?
  • How is the gradient related to the power supplied to the solid?
A
  • The gradient (ΔT/Δt)[solid] is the rate of increase of the temperature of the solid.
  • Related to power supplied by:
    • P = mc[solid] (ΔT/Δt) [solid]
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

Look between C and D:

  • What is represented by the gradient?
  • How is the gradient related to the power supplied?
A
  • Gradient, (ΔT/Δt) [liquid] = rate of change of temperature.
  • Gradient is related to the power supply by:
    • P = mc[liquid] (ΔT/Δt) [liquid]
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

Why are the gradients of this graph for solid, liquid and gas phases not necessarily the same?

A
  • Gradient = Rate of change of temperature , (ΔT/Δt)phase
  • Power = mcphase (ΔT/Δt)phase
  • So, assuming constant power,
    • Gradient ∝ 1/(specific heat capacity)Phase
  • ∴ If the liquid phase has Cliquid < Csolid then the liquid heats up faster than the solid → steeper gradient.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

What is an expression for the

  • melting time
  • boiling time

in this scenario?

A
  • For a change of phase at constant temperature,
    • ΔQ = m l fusion or vaporisation = P Δt
  • ∴ melting or boiling time = (m l fusion or vaporisation )/ Power
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

Which ‘heat equation’ is true in this situation:

  • When a substance’s temperature changes when heat is transferred
  • Phase does not change
A
  • ΔQ = mc ΔT ‘holds’/equals the energy transferred
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

Which ‘heat equation’ holds in this situation:

  • When a substance’s phase changes when heat is transferred,
  • … and its temperature stays constant:
A
  • ΔQ = ml
    • where l is either the latent heat of fusion (lf) or the latent heat of vaporisation (lv).
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

(Exam tech) If in any situation the volume of

the substance is given __________________

A

convert this into the mass by using V𝜌 = m

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

What is the temperature of steam (specifically referring to water in the gas phase, formed when water boils).

A

At atmospheric pressure, steam always has a temperature of 100℃.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
35
Q

When a substance changes phase from a solid to a liquid, when is this latent heat of fusion released?

A
  • LHF (supplied during phase transition from solid → liquid) is released when a liquid solidifies.
  • During solidification (liquid → solid)
    • Liquid’s molecules slow down
    • mean KE ↓
    • Molecules unable to overcome ‘force bonds’
      • ∴ start to lock molecules into fixed positions of a solid
  • Some of the latent heat released during solidification keeps temperature at melting point, until all the liquid has solidified.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
36
Q

Why is it called the “latent” heat of fusion/vaporisation?

A
  • “Latent” = “Hidden”
  • Latent heat supplied to melt any solid can be considered ‘hidden’
    • ∵ no temperature change takes place,
    • Even though the solid is being heated
    • (and its internal energy is increasing therefore).
  • Fusion = the term referring to the melting of a solid.
  • Vaporisation = term referring to boiling of a liquid.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
37
Q

Explain what happens when a liquid is heated near its boiling point.

A
  • The molecules gain enough kinetic energy to overcome intermolecular forces between them (which previously held them close together as a liquid), and to break away from from being ‘in contact with each other’.
  • Liquid molecules gain enough KE
    • .. Able to overcome intermolecular forces between them
      • (Which previously held them close together - liquid).
      • Now able to become separated by rel. large distances
  • Energy required to vaporise any mass of liquid → gas at constant temperature is called ‘latent heat of vaporisation’
  • This latent heat of vaporisation (= m l V) released again when a vapour condenses.
38
Q

Explain in molecular terms the process of a vapour condensing.

A
  • As the vapour’s temperature↓ to boiling point.
    • Vapour molecules <ke>↓</ke>
  • Molecules eventually have low enough <ke>
    </ke><ul>
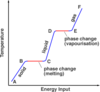
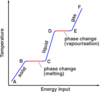
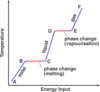
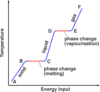
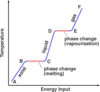
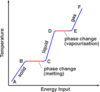
    <li>Intermolecular forces able to pull molecules together to form a liquid.</li>
    </ul></ke>
39
Q

What is sublimation

A

Sublimation is the process whereby a solid vaporises directly into a solid when heated.

40
Q

Compare the size of:

  • Specific latent heat of fusion (lF)
  • Specific latent heat of vaporisation (lV)
A

In general:

  • Specific Latent Heat of Fusion << Specific Latent Heat of Vaporisation
  • “The specific latent heat of vaporisation of a substance is always much greater than the specific latent heat of fusion”
  • Example:
    • For 1 kg of water (S)LHV = 2.25 MJ, much larger than its (S)LHF = 0.336 MJ.
41
Q

What is the specific latent heat of fusion: lF

A
  • The energy needed…
  • …. to change unit mass of the substance …
  • …from solid to liquid…
  • … without changing its temperature.
42
Q

How is the energy of a molecule in a solid substance affected by:

  • Heat transfer to the solid which results in increased temperature.
A
  • Heat energy transferred to ↑temperature of the solid:
    • Causes ↑<ke> of solid's molecules.</ke>
43
Q

How is the energy of a molecule in a solid substance affected by:

  • Heat transfer to the solid which results in the solid melting (‘fusing’).
A
  • Energy supplied during the melting of a solid
    • goes towards increasing the potential energy of the solid’s molecules
    • because they break free from each other
    • — potential energy increases (since work has to be done against forces of attraction between the molecules in the solid’s 3D structure).
  • When a substance is melting (or fusing),
    • the energy supplied does not raise the temperature.
    • All the energy supplied is used to break intermolecular force bonds and change the phase.
    • The energy input becomes internal potential energy. <v></v>
44
Q

What are the molecular properties of liquids?

A
  • Liquids have higher internal energy than solids.
    • Relatively weak Intermolecular forces between liquid’s molecules not strong enough to hold molecules in fixed positions (as in solid phase).
  • Molecules in random motion, able to change relative positions.
    • But unable to become separated from each other.
  • Heat/Work into liquid → Increased Liquid Temperature (TE↑) → increased (∵ molecular speed↑).
  • Liquid vaporises if sufficient energy is supplied because eventually the molecules will have sufficient KE + PE to break free ad move away from other molecules.
    • Therefore lower KE and PE than the gas phase.
45
Q

What are the molecular properties of a gas?

A
  • Very weak intermolecular attraction between gas molecules.
  • Particles separated by relatively large distances (relatively high PE therefore) ∴ Vol1 kg liquid much less than Vol1 kg gas of a substance.
  • High <ke> , molecules moving at high speeds.</ke>
  • Internal energy = KE + PE,
    • So ↑U →
      • higher temperature
      • higher pressure (assuming constant vol. and mass).
46
Q

How could ↑U of a gas result in higher:

  • Pressure
  • Temperature

assuming constant volume and mass.

A
  • ↑U means ↑KE or ↑PE of molecules.
    • ↑KE → higher temperature
    • ↑PE → greater separation between molecules → higher pressure
47
Q

Why does the temperature of a gas change when

  1. It does work e.g. by pushing out a piston by increasing in volume.
  2. Work is done on it, e.g. compression by a piston
A
  • Piston may compress or expand a constant mass of gas.
  • Compression:
    • Piston does mechanical work on the gas, ΔW = P ΔV for small ΔV.
    • ↑U → ↑Temperature
  • Expansion
    • Gas does mechanical work on piston as it expands in volume.
    • ↓U causing decrease in temperature.
  • Effectively this is a way of converthing the gas’s internal energy into mechanical work.
48
Q

What is thermal equilibrium?

A
  • When there is no overall heat transfer…
  • … between objects at the same temperature.
49
Q

What’s an example of a system omving towards thermal equilibrium.

A
  • Placing an object in higher/lower temperature water → heat transfer to/from the object → reduces temperature difference
    • Moves towards thermal equilibrium
  • If water is at same temperature as the object
    • No temperature difference
    • ∴ no overall heat transfer occurs.
50
Q

What is a

  • Molecule
  • Atom
A
  • Molecule: smallest particle of a substance that is characteristic of the substance.
  • Atom: the smallest particle of an element that is characteristic of the element.
51
Q

Compare the volume occupied by 1 kg of a substance

  • In gas phase,
  • In liquid phase
A
  • The 1kg of gas occupies much more volume than the same matter in liquid phase.
  • ∵ Gas molecules have much larger distances between them.
52
Q

How does a gas exert pressure on its container?

A
  • Gas molecules
    • Constantly moving at high speed
  • Make frequent elastic collisions with container walls
    • i.e. without KE loss.
  • During rebound, momentum of particles changes
    • Change in momentum over a period of time occurs,
    • ∴ A force acts on the rebounding molecule (N2L)
    • ∴ The molecule exerts a force on the container wall (N3L)
  • Numerous molecular collisions over the area of container surface produce macroscopic gas-pressure.
53
Q

Describe the molecular structure and properties of a solid

A

Molecules :

  • Organised in a regular 3D structure.
  • Have ‘strong’ intermolecular forces attraction between them.
  • Vibrate randomly about fixed points, but cannot move out of position in structure.
54
Q

Explain in molecular terms the process of a solid melting.

A
  • Heating a solid increases KE of molecules.
    • Molecules have higher speed/vibrate faster
  • With enough energy… molecules can be made to :
    • Break out of positions
    • Move around freely.
  • … solid melts into a liquid.
55
Q

What holds molecules attracted to each other in a solid?

A
  • Intermolecular forces
    • Arise from the electrical charges of the protons/electrons in constitutent molecules.
56
Q

What relates the temperature of a solid, and the rate at which its molecules vibrate?

A
  • ↑Temperature → ↑ ∴ faster vibration.
57
Q

What happens when heat is continuously added to a substance in solid phase?

A
  • Temp.↑ up to melting point.
  • Temp. stays at MP until latent heat of fusion transferred.
    • Meanwhile phase changes to liquid.
  • Liquid temp↑ up to boiling point.
  • Temp. stays at BP until latent heat of vaporsiation transferred
    • Meanwhile phase change from liquid to gas.

Note: BP and MP only well defined temperatures for pure substances.

58
Q

What happens when heat is transferred to steam in a piston

  • When the volume is held constant.
  • When the pressure is held constant (atmospheric pressure)
A
  • Constant volume:
    • ΔU = ΔW + ΔQsupplied
    • Vol constant, ∴ΔW = 0
    • ΔU = ΔQsupplied<strong> </strong>→ temperature of the gas increases
      • In turn implies pressure of gas must have increased.
  • Constant atmospheric pressure → temp. of steam ≡ 100℃ ∴ isothermal conditions,
    • (Assuming no heat loss to surroundings is allowed
      • ΔU = ΔW + ΔQsupplied
      • Isothermal → ΔU = 0 → ΔW = - ΔQsupplied , so gas does work on surroundings.
      • Piston is pushed out by the expanding gas, doing mechanical work equal to ΔQsupplied
59
Q

Compare the 𝜌 of a gas with the 𝜌 of a liquid / solid.

A
  • 𝜌[gas] <<< 𝜌[liquid] < 𝜌[solid]
  • Molecules of Liquid/Solid packed ‘in contact’ together without much distance separating them.
  • Gas molecules typically spaced far apart on average by relatively large distances.
60
Q

Why are liquids / gases fluid while solids are not?

A
  • Solid:
    • molecules prevented from moving relative to another by strong force bonds.
  • Liquids/Gases:
    • molecules have too much KE/PE allowing them to overcome (to varying extents) the attraction of the forces between molecules,
    • allowing the molecules to move relative to one another and exhibit fluid behaviour on a macroscopic scale.
    • The force bonds are not strong enough to keep the molecules fixed to each other.
61
Q

Explain in terms of molecules what happens when a solid or liquid is heated (when not near its melting/boiling points).

A
  • Solid → ΔQ → molecules vibrate more quickly about fixed positions (mean positions)
  • Liquid → ΔQ → molecules move more quickly relative to each other, still keep in contact with each other but free to move about.
62
Q

What happens when a solid is heated near its melting point?

A
  • Energy is needed to break bonds when a substance changes phase.
  • This energy is called latent heat,
    • and temperature of a substance remains constant during a change of phase.
  • The energy needed for a change of state is calculated as follows
    • ΔQ = mlFUSION
63
Q

How can you adapt the equation for heat capacity to the number of moles in a substance (Rather than the mass).

A
  • It is sometimes more convenient to relate heat capacity to the number of moles of a substance rather than its mass in kg.
  • The specific heat capacity equation then becomes
    • ΔQ = nCΔT
  • and the latent heat capacity equation becomes
    • ΔQ = nL

Where

  • ΔQ Heat energy transferred, J
  • n Number of moles, mol
  • C Molar heat capacity, J mol-1 K-1
  • Lf or v Molar latent heat of fusion or vaporisation, J mol-1
  • ΔT Temperature change, K
64
Q

Give an example of how different substances can heat up at different rates

A
  • On a beach during a warm day, the sand may become extremely warm wile the water remains refreshingly cool.
  • Sand and water have different specific heat capacities.
65
Q

What are the 3 factors which affect the temperature rise (Δt) of an object when it is heated with a certain amount of heat energy transferred to the object (ΔQ).

A
  • The mass of the object.
  • The amount of energy supplied to it.
  • The specific heat capacity of the substance (c) from which the object is made.
66
Q

Define ‘specific heat capacity’, c, of a substance.

A
  • Specific heat capacity of a substance is the energy needed to raise the temperature of unit mass (1 kg) by 1 Kelvin without change of state.
  • Unit: J/kg/K
67
Q

Give the equation and derivation of the relationship between m, ΔE, c, ΔT.

A

To raise the temperature of mass m of a substance from temperature T1 to temperature T2:
Energy needed, ΔQ = mc(T2 — T1) = mc ΔT where ΔT = T2 — T1
2. *Derivation?

68
Q

What are the issues of applying the specific heat capacity equation to a gas

A
  • Specific Heat Capacity of a Gas: This can take any value depending on how much the gas expands during heating.
  • Also, the specific heat capacity of a gas in state changes at constant pressure is greater than state changes occurring with constant volume.
69
Q

Describe the inversion tube expriment

A

The Inversion Tube Experiment

  • Setup: Vertical Tube of length L with facility of inserting a thermometer to measure temperature.
  • Inverting tube causes GPE of object within to be transformed: ΔGPE —> ΔKE —(work)—> ΔU
  • Purpose is to experimentally determine the specific heat constant of the solid object within.
70
Q

Derive an expression for the specific heat capacity in the context of the inversion tube experiment.

A
  • Mass of lead shot used := m
  • Tube Length := L
  • Inversions := n

Analysis

  • ΔGPE each inversion = mgL —> ΔGPE = n.m.g.L
  • ΔGPE lead shot —> ΔU lead shot [assumption]
  • = ΔQ
  • n.m.g.L = ΔQ = mc ΔT, ΔTof lead shot = T2 — T1
  • n.g.L = c ΔT
  • c = n.g.L/ΔT allows you to calculate the specific heat capacity of the lead shot.
71
Q

Describe the experimental setup for measuring the specific heat capacity using experimental methods.

A
  • Metal block, mass = m, contained within an insulated container.
    • 1st Hole drilled inside metal and a 12v electrical heater is inserted into it.
    • Supplies known amount of electrical energy
  • Circuit: cell, switch, veristor, ammeter, voltmeter (in parallel with heater)
  • 2nd hole — thermometer inserted into the metal
    • Measures temperature ΔT = T2 — T1
  • Small amount of water/oil inserted into the metal improves the thermal contact between the thermometer
72
Q

How can you calculate the SHC of a metal using the electrical method (knowing P, I, V of heater, and having measured the heating time?).

A

Heater —> {P, I, V}

{t = heating time]

  • P = IVt = ΔQ
  • = mc ΔT
  • c = (IVt)/(mΔT) is an alternate way of calculating the specific heat capacity.
73
Q

Describe the experiment for measuring the specific heat capacity of a liquid

A
  • Use same circuit as electrical method - with heater.
  • Liquid (known mass m L but unknown specific heat capacity cL) placed in a calorimeter (of known mass mc and specific heat capacity cc) assuming no heat loss of calorimeter.
  • Liquid is heated directly using 12v electrical heater.
  • Thermometer inserted into liquid to measure temperature change ΔT [stir liquid before measurement].
74
Q

Describe how to calculate the specific heat capacity CL of a liquid knowing

  • Mass of liquid,
  • Mass and C of calorimeter
  • Temperature change of Liquid and Calorimeter
A
  • E supplied = IVt = current ⨉ pd ⨉ heating time
  • E —> ΔU liquid + ΔU calorimeter (where U generally stands for internal energy).
  • = mLcLΔT + mcccΔT assuming both calorimeter and liquid undergo same ΔT, and there’s no heat loss to surroundings.

So: IVt = mLcLΔT + mcccΔT

  • All quantities except cL are known/ can be determined experimentally.
75
Q

Apply the equation relating temperature change and work done on the solid/liquid to a continuous flow heating process.

A

(ΔQ/Δt) = (Δm/Δt) c (T2 - T1)

Where ΔQ/Δt = Heat energy transferred to the fluid per second [J/s]
Δm/Δt = Mass flow rate of the liquid per second [kg/s]
c = Specific heat capacity of fluid, J kg-1K-1
T1 & T2 : Temperature of fluid before and after heating, K.

76
Q

Explain the concept of a temperature scale

A
  • Defined in terms of two ‘standard’ fixed point temperatures
  • …. which are standard degrees of hotness
  • …. which can easily and accurately be reproduced.
77
Q

Standard fixed points of the Celsius scale:

A
  • Ice point 0℃ — the temperature of pure melting ice.
  • Steam point 100℃ — the temperature of steam at standard atmospheric pressure.
78
Q

What are the fixed points of the Kelvin (or ‘Absolute’) temperature scale.

A
  • Absolute zero: 0K, the lowest possible temperature associated with minimum internal energy.
  • Triple point of water: 273.15 K the temperature at which water, ice and water vapour coexist in thermodynamic equilibrium (i.e. no heat flow).
  • Therefore Temperature in oC = Absolute temperature in K – 273.15
79
Q

Explain the concept of ‘absolute zero’

A
  • An object at absolute zero has minimum internal energy, regardless of the substances that the object consists of.
  • Therefore no object can have a temperature below absolute zero.
80
Q

Explain how absolute zero is determined experimentally.

A
  • Take a fixed mass of gas and a fixed volume sealed container.
  • Measure gas pressure as temperature changes
  • Line of best fit always cuts the temperature axis at -273℃, regardless of which gas is used or how much gas is used.
81
Q

State some of the ways in which the properties of matter change at very low temperatures:

A
  • Superconductivity - zero resistivity.
  • Superfluids - can empty themselves out of containers.
  • These properties become apparent when matter is cooled to a few micro-Kelvin of absolute zero, which can be achieved in laboratories using scientific approaches.
82
Q

Explain the Zeroth Law of Thermodynamics

A

(1) If two systems are at the same temperature, there is no resultant flow of heat energy between them.

83
Q

Give an example to illustrate the Zeroth Law of Thermodynamics

A

Example: is well illustrated by goldfish.

  • Fish are cold blooded so they are at the same temperature as the water.
  • Because there is no flow of heat energy between them we say that they are in thermal equilibrium.
  • This is the zeroth law… ‘if two systems are at the same temperature, there is no resultant flow of heat between them”
84
Q

Explain the 1st Law of Thermodynamics.

A

1st Law of Thermodynamics: Is a conservation of energy law, showing that if you add heat or work to a system its internal energy increases.

∆U of system = ∆Q into system + ∆W on system.

Be accurate with direction of work / heat energy transfers.

85
Q
  • Explain
    • (a) what an isothermal change is, and
    • (b) what this implies about the link between work done on/by an object and heat transfer in/out of an object.
A
  • An isothermal change is a change in state which occurs at constant temperature, i.e. no change in internal energy.
  • If ΔU = 0, and ΔU = ΔQ+ΔW,
    • then ΔW = -ΔQ,
  • i.e. In an isothermal situation if work is done on a system, an equal amount of heat must be lost from the system.
86
Q
  • Explain
    • (a) what is meant by an adiabatic situation and
    • (b) What this implies about the relationship between ΔW and ΔQ.
A
  • An adiabatic situation means no energy is lost to the surroundings.
  • This usually happens because adiabatic changes occur so quickly that there is no time for a system to lose heat to the surroundings.
  • Thus ΔQ = 0 &
    • ΔU = ΔW
87
Q

Illustrate an adiabatic situation with an example?

A
  • An adiabatic change in which work is done on the system (i.e. system is compressed) results in increased internal energy & thus increased temperature.
  • An adiabatic change in which work is done by the system (i.e. system expands) results in decreased internal energy & thus reduced temperature.
88
Q

Explain the relationship between ΔU and ΔQ, ΔW when Volume is held constant (and other state variables change). Apply this concept.

A
  • In a constant volume change,
    • no work is done because force (arising from gas pressure) does not move across a distance.
    • Thus ΔW = 0 and ΔU = ΔQ.
  • The heating of a solid or liquid is, more or less, a constant volume state change.
  • Although liquids do expand more than a solid under heating,
    • the work done in pushing back the surroundings is small compared with the energy needed to change the kinetic energy (& temperature) of the molecules.
89
Q

Derive an expression for the work done ΔW in compressing a gas at pressure P resulting in a volume change of ΔV in a cylindrical piston of cross sectional area A.

A

ΔW = F Δs
P = F/A
F = PA
ΔW = P (A Δs) = P ΔV
Hence ΔW = P ΔV
Work Done = Pressure ⨉ Change in Volume
[J] [N/m2] x [m3]

Note: only applies for small volume changes as pressure changes with volume.

90
Q
A
91
Q
A

A2 Physics Knowledge (5 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions