03 Crystallography, Structure of Crystalline Solids

Question 1

1. Give a definition of crystalline solid.

Answer 1

a crystalline material is one in which the atoms are situated in a repeating or periodic array over large atomic distances

Question 2

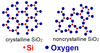
2. Describe the difference in atomic/molecular structure between crystalline and noncrystalline materials.

Answer 2

atoms in crystalline solids are positioned in orderly and repeated patterns that are in contrast to the random and disorderd atomic distribution found in noncrystalline (=amorphous) materials

Question 3

3. Give a brief definition of a unit cell.

Answer 3

Crystalline solids consist of small groups of atoms which form a repetitive pattern. In describing crystal structures, is is often convenient to subdivide the structure into small repeat entities called unit cells. Most unit cells are parallelepipeds (Spat) with three sets of parallel faces.

Question 4

4. Draw unit cells for face-centered cubic, body-centered cubic, and hexagonal close-packed crystal structures.

Answer 4

A…body-centered cubic BCC e.g. Cr, Fe (α), tungsten W

B…face-centered cubic FCC e.g. Al, Cu, Au, Ag, Pb,
stacking sequence: ABCABC…

C…hexagonal close-packed structure HCP e.g. Cd, Co, Ti(α), Zn

stacking sequence: ABAB…

Question 5

5. Derive the relationships between unit cell edge length and atomic radius for face-centered cubic and body-centered cubic crystal structures.

Answer 5

Question 6

6. Given the atomic radius of an atom which forms into a face-centered cubic crystal structure as well as the metal’s atomic weight, compute its density.

Answer 6

In order to get the density we nee the volume of the unit cell. Given the atomic radius R for an FCC structure, the unit cell edge length becomes a = 2*sqrt(2)*R. Hence we get V = a³. Mass of Atoms in the unit cell is calculated as shown below:

Question 7

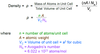
7. Given the atomic radius of an atom which forms into a body-centered cubic crystal structure as well as the metal’s atomic weight, compute its density.

Answer 7

a = 4*R*1/sqrt(3), V=a³

Not that atomic weight A = [amu/atom(molecule) = g/mol]
1 amu = 1/12 of C¹² - isotope

Question 8

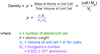
8. (a) Explain what is meant by coordination number and atomic packing factor.

Answer 8

Two important features of a crystal structure are:

1. Coordination number: the number of nearest-neighbor or touching atoms
2. Atomic packing factor (APF): the fraction of solid-sphere volume in the unit cell

Question 9

8. (b) Cite the atomic packing factors and coordination numbers for body-centered cubic, face-centered cubic, and hexagonal close-packed crystal structures.

Answer 9

• BCC: APF = 0.68, Coord# = 8, 2 atoms/unit cell
• FCC: APF = 0.74, Coord# = 12, 4 atoms/unit cell
• HCP: APF = 0.74, Coord# = 12, 6 atoms/unit cell
• simple cubic: APF = 0.52, Coord# = 6, 1 atom/unit cell

Question 10

9. Briefly define polymorphism (or allotropy).

Answer 10

Polymorphism occurs when a specific material can have more than one crystal structure. Allotropy is polymorphism for elemental solids.

Question 11

10. Distinguish between crystal system and crystal structure.

Answer 11

the concept of crystal system is used to classify crystal structures on the basis of unit cell geometry - that is unit cell edge lengths and interaxial angles. There are 7 crystal systems:

1. cubic
2. tetragonal
3. hexagonal
4. orthorhombic
5. rhombohedral (trigonal)
6. monoclinic
7. triclinic

Question 12

11. Recognize and also give the lattice parameter relationships for all seven crystal systems–i.e., cubic, hexagonal, tetragonal, rhombohedral, orthorhombic, monoclinic, and triclinic.

Answer 12

Question 13

12. Given a unit cell and three point coordinates, locate the point represented by these indices within the unit cell.

Answer 13

done by point coordinates q, r, and s
q in a-direction (x-axis)

r in b-direction (y-axis)

s in c-direction (z-axis)

Question 14

13. Given the location of a point within a unit cell, specify its point coordinates.

Answer 14

1. Lattice position/coordinates are known in a metric scale: a, b, and c (e.g.[nm])
2. Divide by unit cell edge lengths a, b, c and remove commas to obtain the point coordinates.

e. g. a = 0.12nm, b = 0.46nm, c = 0.20nm and
* a* = 0.48nm, b = 0.46nm, and c = 0.40nm we get:

point coordinates: 1/4 1 1/2

Question 15

14. Given three index integers, sketch the direction corresponding to these indices within a unit cell (for all crystal systems).

Answer 15

Question 16

15. Given a direction that has been drawn referenced to a unit cell (for all crystal systems), specify its direction indices.

Answer 16

Question 17

16. Given a unit cell and the Miller indices for a plane, draw the plane represented by these indices referenced to this unit cell.

Answer 17

Miller indices (hkl) are refered to all crystal systems except the hexagonal one.

reciprocal terms (n is an appropriate factor):

h = n* a/A

k = n* b/B

l = n* c/C

Question 18

17. Specify the Miller indices for a plane that has been drawn within a unit cell.

Answer 18

Question 19

20. Given the unit cell for some crystal structure, be able to draw the atomic/ionic packing arrangement for a specific crystallographic plane.

Answer 19

Question 20

21. Define both linear and planar atomic densities.

Answer 20

linear:
number of atoms centered on the direction vector divided by the length of the dircetion vector

planar:
number of atoms centered on a plane divided by the area of the plane

Question 21

22. For a given crystal structure, be able to determine the linear density for a specified crystallographic direction.
23. For a given crystal structure, be able to determine the planar density for a specified crystallographic plane.

Question 22

24. (a) Draw the packing of a close-packed plane of spheres (atoms).

Answer 22

?

Question 23

(b) Describe how both hexagonal close-packed and face-centered cubic crystal structures may be generated by the stacking of close-packed planes of atoms.

Do the same for the sodium chloride crystal structure in terms of closed packed planes of anions.

Answer 23

FCC and HCP crystal structures can be generated by the stacking of closed packed planes of atoms on top of each other. With this scheme A, B, and C denote possible atom positions on a close packed plane.

Stacking sequence for HCP is ABABAB…

Stacking sequence for FCC is ABCABCABC…

The same happens in some ceramic crystal structures (e.g. NaCl) by stacking of close-packed planes of anions; cations fill interstitial tetrahedral and/or octahedral positiions that exits between adjacent planes.

Question 24

(c) Cite which planes in both hexagonal close-packed and face-centered cubic structures are close-packed.

Answer 24

close packed planes for FCC and HCP are {111} and {0001}, respectively

Remark:

Family of directions –all directions that are crystallographically equivalent (have the same atomic spacing) –indicated by indices in angle brackets

e.g. <100> = [100],[010],[001],[-100],[0-10],[00-1]

Family of planes –all planes that are crystallographically equivalent (have the same atomic packing) –indicated by indices in braces

e.g. {100} = (100), (010), (001), (-100), (0-10),(00-1)

Question 25

25. Distinguish between single crystals and polycrystalline materials.

Answer 25

single crystals are materials in which the atomic order extends uninterrupted over the entirety of the specimen (which can lead to flat faces and regular geometric shapes)

The vast majority of crystalline solids are polycrystalline i.e. they´re composed of many small crystals or grains having different crystallographic orientations.

Question 26

26. Define grain boundary.

Answer 26

is the boundary region separating two grains where there is some atomic mismatch

Question 27

27. Define isotropy and anisotropy with respect to material properties.

Answer 27

Anisotropy is the directionality dependence of properties. For isotropic materials, properties are independent of the direction of measurement.

Question 28

28. Briefly describe the phenomenon of diffraction.

Answer 28

diffraction = constructive interference

Two waves that mutually reinforce (=constructively interfer with) on another is a manifestation of diffracton, and we refer to a diffracted beam as one composed of a large number of scattered waves that mutualy reinforce on another.

Question 29

29. Given the angle at which an x-ray diffraction peak occurs, as well as the x-ray wavelength and order of reflection, compute the interplanar spacing for the crystallographic planes that are responsible for the diffraction peak.

Answer 29

see Exercise 2 - Problem 5

Question 30

30. For crystals having cubic symmetry, given the lattice parameter (i.e., unit cell edge length), compute the interplanar spacing for a set of crystallographic planes of specified Miller indices.

Answer 30

interplanar spacing d_hkl

unit cell edge length a