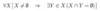0 - Axioms of ZFC Flashcards
What is the name of the following ZFC Axiom?
For all x, for all y (
For all z (
z is in x
iff
z is in y ))
Axiom of Extensionality
For all x, for all y (
For all z (
z is in x
iff
z is in y ))
What is the name of the following ZFC Axiom?
For all x (
There exists a y s.t. y is in x
implies
there exists a z (
z is in x
AND
for all w (
w is in x
implies
w is not in z )))
Axiom of Foundation
For all x (
There exists a y : y is in x
implies
there exists a z (
z is in x
AND
for all w (
w is in x
implies
w is not in z )))
The two regulative axioms are ______** and **_____\_.
These tell you that all sets have these properties, but not if there are any sets to begin with.
The two regulative axioms are extensionality** and **foundation.
These tell you that all sets have these properties, but not if there are any sets to begin with.
What is the name of the following axiom?
For all x, For all y, There exists a z (
x is in z
AND
y is in z )
Axiom of Pairing
For all x, For all y, There exists a z (
x is in z
AND
y is in z )
The axiom of ______\_ says that
if you have 2 sets you can make another set that contains both of these.
The axiom of pairing says that
if you have 2 sets you can make another set that contains both of these.
What is the name of the following axiom?
For all x, There exists a z, For all y, For all w (
( y is in w
AND
w is in x )
implies
y is in z )
Axiom of Union
For all x, There exists a z, For all y, For all w (
( y is in w
AND
w is in x )
implies
y is in z )
The axiom of _____\_ says that you can create a new set z out of the elements of the elements of some set x.
The axiom of union says that you can create a new set z out of the elements of the elements of some set x.
These three axioms are known as the generative or combinatorial axioms because they grant you the ability to create new sets:
These three axioms are known as the generative or combinatorial axioms because they grant you the ability to create new sets:
Pairing, Union, Power Set
What is the name of the following axiom?
For all x, There exists a y, For all z (
For all w
( w is in z
implies
w is in x )
implies
z is in y )
Power Set
For all x, There exists a y, For all z (
For all w
( w is in z
implies
w is in x )
implies
z is in y )
What is the name of the following axiom?
For all w, There exists a y, For all z
( z is in y
iff
z is in w
AND
phi(z) )
where phi(z) is an arbitrary formula in the language of relations
Axiom (Schema) of Separation
For all w, There exists a y, For all z
( z is in y
iff
z is in w
AND
phi(z) )
where phi(z) is an arbitrary formula in the language of relations
The axiom of ________\_ allows you to create or partition a subset from a set as long as you can declare a property that it has.
The axiom of separation allows you to create or partition a subset from a set as long as you can declare a property that it has.
What is the name of the following axiom?
For all x0…x1 (
For all u,
There exists a unique z with the property phi(z),
implies
For all w, There exists a u, For all y
(y is in w
iff
there exists a z
( z is in u
AND
phi (y, z, x0…x1 )))
Axiom of Replacement
For all x0…x1 (
For all u,
There exists a unique z with the property phi(z),
implies
For all w, There exists a u, For all y
(y is in w
iff
there exists a z
( z is in u
AND
phi (y, z, x0…x1 )))
This axiom contains the statement that there is only one x that satisfies some uniqueness and existence principle y:
This axiom contains the statement that there is only one x that satisfies some uniqueness and existence principle y:
Replacement
What is the name of the following axiom?
There exists an x
( There exists a y s.t. y is in x
AND
For all z
( z is in x
implies
There exists a w
( z is in w
AND w is in x )))
Axiom of Infinity
There exists an x
( There exists a y s.t. y is in x
AND
For all z
( z is in x
implies
There exists a w
( z is in w
AND w is in x )))
This is the only axiom that starts with an existential operator:
This is the only axiom that starts with an existential operator:
Axiom of Infinity
The axiom of ______\_ states that the elements of elements of a set x can create a new unique set that is composed of the pairwise disjoint elements of each.
The axiom of choice states that the elements of elements of a set x can create a new unique set that is composed of the pairwise disjoint elements of each.
For proving that a set with some condition exists you first have to prove ________** and **_______\_.
You usually use some combination of axioms to prove the first, and then follow it up with the axiom of _____\_ to prove the latter.
For proving that a set with some condition exists you first have to prove existence** and **uniqueness.
You usually use some combination of axioms to prove the first, and then follow it up with the axiom of extensionality to prove the latter.
What is this axiom?

Extensionality

What is this axiom?

Pairing

What is this axiom?

Union

What is this axiom?

Empty Set

What is this axiom?

Infinity

What is this axiom?
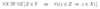
Power Set
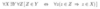
What is this axiom?

Replacement