Yohance Defns Flashcards
Defn of a subset U being open

Defn of neighbourhood

Defn of Function being continious

Defn of subset being compact

Details of mobius transformation

Defn of function being analytic (power series)

Defn of CR eqns in both real form and imaginary form

Defn of partial derivative wrt to z and z*
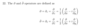
Defn of a function u(x,y) being harmonic

defn of v being harmonic conjugate to u

Defn of a curve being closed

Suppose f is continious and gamma is a smoth curve, define the intergral of f.
also define the parametiztion f = P +iQ

Define L(z)
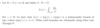
statement about polynomials factorisaiton and zeros, with order of zeros

Defn of isolated singularity

Defn of Laurent Expansion. When is z_0 a removable singularity? defn of pole of order m?
defn of essential singularity?

If z_0 is an isolated singularity, defn the principle part

Define the residue of f at z_0

Define the principle part of z_0 if;
i) singularity is removable
ii) singularity is a pole
iii) in the case of an essential singularity

Defn of entire. Defn of meromophic

Statement about continuity of f(z) where f(z) is described as a power series

Maclaurin Taylor expansion of f(z)

Requirment of conformality of a function f(z)

if f’(z) = 0 for all z in complex plane then …

Suppose u is harmonic in complex plane, give statement about existence of v

State Triangle inequality for intergrals

State ML Lemma

Give statement about path independence of intergral

State Fundamental Thm of Calculus for complex plane

give statement about existance of F’(z) = f(z)

State Cauchys Thm

State Cauchys Intergral Formula

state result about intergral of 1/(z-a) along curve |z|=R for |a| > R and |a| < R

State Cauchys formula for its derivatives

Describe f as its taylor expansion and cauchy inequalities

State Louivilles Thm

State Fundemental Thm of Algebra

Give statement about zeros of non-zero polynomials

State Laurents Theorem

State Residue Theorem for Meromorphic functions

Suppose f(z) = h(z)/g(z) , give details about resiude of such function

Suppose f(z) = g(z) / (z-z_0)^m, give statement about residue of pole

State Jordans Lemma

State Rouches Thm



