Whole Year Flashcards
What is the limit definition of an integral?

What is the limit defintion of a derivative?
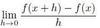
What is the derivative of an inverse function with a variable of y?

What is the limit as x approaches zero of (sin(x))/x ?
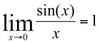
What does intermediate value theorem state about continuous functions?
If f is continuous on an interval [a,b], and a number k is between f(a) and f(b), there will be at least one number c such that f(c)=k.
For example, any continuous function over [a,b] for which f(a) is negative and f(b) is positive, there must be at least one x intercept on the interval [a,b].
What are the derivatives of:
sin(x)
cos(x)
tan(x)
cos(x)
-sin(x)
sec2(x)
True or false?
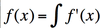
False! Never forget the dx on an integral!
“a” is a function representing the acceleration of a particle with linear motion. If the particle’s position at t=0 is +24 units from the origin, write a function for the particle’s position at any time “t”.
a(t)=-cos(t)+6
s(t)=cos(t)+3t2+23
What is the derivative of ex?
ex
According to the fundamental theorem of calculus, what is this equation equal to?
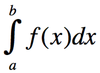
F(b)-F(a), F being the antiderivatve of f.
According to the Fundamental Theorem of Calculus, what does this equation equal?
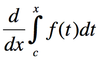
f(x)
Find the limit as x approaches zero.
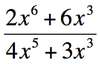
2
Find the limit as x approaches infinity.
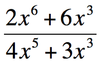
Infinity.
For what value of x does the function f(x)=2x3-3x2-12x have a relative minimum?
2
R is a differentiable function in terms of t, that gives how much rain has fallen over the course of a 3 day period. t is in hours. What is represented by R’(36)?
The rate at which the amount of rain fallen is changing at the end of the 36th hour (instantaneously).
Find the area between f(x)=2x-x2 and g(x)=x2
1/3
Use summation notation to write the right Riemann sum for n, for the integral from 0 to 3 of (2x-5) dx.
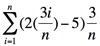
Find the second derivative of f(x)=x4-2x3+cos(-2x)
f’‘(x)=12x2-12x+4cos(-2x)
Find the first derivative of f(x)=log3(x2)
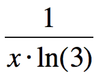
Find the derivative of f(x)=cos(x)sin(x)
-sin2x+cos2x
What is the derivative of f(x)=xn?
f’(x)=nxn-1
What is the definition of an even function?
f(-x)=f(x)
What is the definition of an odd function?
f(-x) = -f(x)
Use the formula for the volume of a sphere to find the formula for the surface area. (Hint: V’=Area)
V=(4/3)πr3
A=4πr2
Find the derivative of (x2-2)/(x3)



