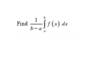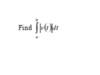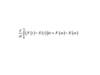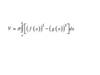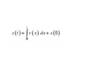When You See...Think Flashcards
Find the zeros
Find roots. Set function = 0, factor or use quadratic
equation if quadratic, graph to find zeros on calculator
Show that f (x) is even
Show that f (−x) = f ( x )
symmetric to y-axis
Show that f (x) is odd
Show that f (−x) = − f (x) OR f (x) = − f (−x)
symmetric around the origin
Show that lim f (x) exists
x-> a
Show that lim f (x )= lim f (x ); exists and are equal
x->a- x->a+
Find lim f ( x ) , calculator allowed
x->a
Use TABLE [ASK], find y values for x-values close to a
from left and right
Find lim f ( x ) , no calculator
x->a
Substitute x = a
1) limit is value if b/c, incl. 0/c=0; c cannot equal 0.
2) DNE for b/0
3) 0/0 DO MORE WORK!
a) rationalize radicals
b) simplify complex fractions
c) factor/reduce
d) know trig limits
1. lim sinx/x= 1
x-\>0
2. lim 1-cosx/x= 0
x-\>0
e) piece-wise function: check if RH = LH at break
Find lim f ( x ) , calculator allowed
x →∞
Use TABLE [ASK], find y values for large values of x,
i.e. 999999999999
Find lim f ( x ) , no calculator
x →∞
Ratios of rates of changes
1) fast/slow= DNE
2) slow/fast= 0
3) same/same= ratio of coefficients
Find horizontal asymptotes of f (x)
Find lim f ( x ) and lim f ( x )
x →∞ x → −∞
Find vertical asymptotes of f (x)
Find where lim f ( x ) = ±∞
x-\>a±
1) Factor/reduce f (x ) and set denominator = 0
2) ln x has VA at x = 0
Find domain of f (x)
Assume domain is (−∞, ∞). Restrictable domains:
denominators ≠ 0, square roots of only non-negative
numbers, log or ln of only positive numbers, real-world
constraints
Show that f (x) is continuous
Show that…
1) lim f(x) exists (limf(x)=limf(x))
x-\>a x-\>a- x-\>a+
2) f (a) exists
3) lim f ( x ) = f (a )
x→a
Find the slope of the tangent line to f (x ) at
x = a.
Find derivative f ′(a ) = m
Find equation of the line tangent to f ( x ) at
( a, b )
f ′(a ) = m and use y − b = m ( x − a )
sometimes need to find b = f ( a )
Find equation of the line normal
(perpendicular) to f (x ) at ( a, b )
Same as above but m =
−1/f ′(a )
Find the average rate of change of f ( x ) on
[a, b]
Find (f (b ) − f (a ))/(b-a)
Show that there exists a c in [a, b] such that
f (c) = n
Intermediate Value Theorem (IVT)
Confirm that f ( x ) is continuous on [a, b] , then show that
f (a) ≤ n ≤ f (b) .
Find the interval where f ( x ) is increasing
Find f ′(x ) , set both numerator and denominator to zero
to find critical points, make sign chart of f ′( x ) and
determine where f ′( x ) is positive.
Find interval where the slope of f (x ) is
increasing
Find the derivative of f ′( x ) = f ′′( x ) , set both numerator
and denominator to zero to find critical points, make
sign chart of f ′′( x ) and determine where f ′′( x ) is
positive.
Find instantaneous rate of change of f (x ) at
a
Find f ′(a )
Given s (t ) (position function), find v(t )
Find v(t ) = s ′(t )
Find f ′( x ) by the limit definition
Frequently asked backwards
f ‘(x)= lim f ( x + h) − f ( x)/h or
h-\>0
f ‘(a)= lim f(x)-f(a)/x-a
x-\>a
Find the average velocity of a particle on
[a, b]
Given v(t ) , determine if a particle is speeding up at t = k
Find v ( k ) and a ( k ) . If signs match, the particle is
speeding up; if different signs, then the particle is
slowing down.
Given a graph of f ′( x ) , find where f (x ) is
increasing
Determine where f ′( x ) is positive (above the x-axis.)
Given a table of x and f ( x ) on selected
values between a and b, estimate f ′(c )
where c is between a and b.
Straddle c, using a value, k, greater than c and a value, h, less than c. So f ‘(c) ≈ f(k)-f(h)/ k-h
Given a graph of f ′( x ) , find where f (x ) has
a relative maximum.
Identify where f ′ ( x ) = 0 crosses the x-axis from above to below OR where f ′(x ) is discontinuous and jumps from above to below the x-axis.
Given a graph of f ′( x ) , find where f (x ) is
concave down.
Identify where f ′(x ) is decreasing.
Given a graph of f ′( x ) , find where f (x ) has
point(s) of inflection.
Identify where f ′(x ) changes from increasing to
decreasing or vice versa.
Show that a piecewise function is
differentiable
at the point a where the function rule
splits
First, be sure that the function is continuous at x = a by
evaluating each function at x = a. Then take the
derivative of each piece and show that
lim f ‘(x)=lim f ‘(x)
x->a- x->a+
Given a graph of f ( x ) and h ( x ) = f^-1(x)
find h ‘ ( a )
Find the point where a is the y-value on f ( x ) , sketch a
tangent line and estimate f ‘ ( b ) at the point, then
h ‘(a)= 1/f ‘(b)
Given the equation for f ( x ) and
h ( x ) = f ^-1( x ) , find h ‘ ( a )
Understand that the point ( a, b ) is on h ( x ) so the point
( b, a ) is on f ( x ) . So find b where f ( b ) = a
h ‘(a) = 1/f ‘(b)
Given the equation for f ( x ) , find its
derivative algebraically.
1) know product/quotient/chain rules
2) know derivatives of basic functions
a. Power Rule: polynomials, radicals, rationals
b. e^x ; b^x
c. ln x;logb x
d. sin x;cos x; tan x
e. arcsin x;arccos x;arctan x;sin^−1 x; etc
Given a relation of x and y, find dy/dx algebraically.
Implicit Differentiation
Find the derivative of each term, using
product/quotient/chain appropriately, especially, chain rule: every derivative of y is multiplied by dy/dx; then group all dy/dx terms on one side; factor out dy/dx and solve.
Find the derivative of f ( g ( x ))
Chain Rule
f ′( g ( x )) ⋅ g ′( x )
Find the minimum value of a function on
[a, b]
Solve f ′ ( x ) = 0 or DNE, make a sign chart, find sign
change from negative to positive for relative minimums
and evaluate those candidates along with endpoints backi nto f (x ) and choose the smallest. NOTE: be careful to confirm that f ( x ) exists for any x-values that make f ‘ ( x ) DNE.
Find the minimum slope of a function on
[a, b]
Solve f “ ( x ) = 0 or DNE, make a sign chart, find sign
change from negative to positive for relative minimums
and evaluate those candidates along with endpoints back
into f ‘ ( x ) and choose the smallest. NOTE: be careful to
confirm that f ( x ) exists for any x-values that make
f “ ( x ) DNE.
Find critical values
Express f ′( x ) as a fraction and solve for numerator and
denominator each equal to zero.
Find the absolute maximum of f ( x )
Solve f ′ ( x ) = 0 or DNE, make a sign chart, find sign
change from positive to negative for relative maximums
and evaluate those candidates into f (x ) , also find
lim x->∞ f(x) and lim x->-∞; choose the largest.
Show that there exists a c in [a, b] such that
f ‘(c) = 0
Rolle’s Theorem
Confirm that f is continuous and differentiable on the
interval. Find k and j in [a, b] such that f ( k ) = f ( j ) ,
then there is some c in [k , j] such that f ′(c)= 0.
Show that there exists a c in [a, b] such that
f ‘(c) = m
Mean Value Theorem
Confirm that f is continuous and differentiable on the
interval. Find k and j in [a, b] such that
m= f(k)-f(j)/(k-j), then there is some c in [k,j] such that f ‘(c)=m
Find range of f (x ) on [a, b]
Use max/min techniques to find values at relative
max/mins. Also compare f ( a ) and f ( b ) (endpoints)
Find range of f (x ) on (− ∞, ∞ )
Use max/min techniques to find values at relative
max/mins. Also compare lim f (x ).
x →±∞
Find the locations of relative extrema of
f ( x ) given both f ‘ ( x ) and f “ ( x ) .
Particularly useful for relations of x and y
where finding a change in sign would be
difficult.
Second Derivative Test
Find where f ‘ ( x ) = 0 OR DNE then check the value of
f “ ( x ) there. If f “ ( x ) is positive, f ( x ) has a relative
minimum. If f “ ( x ) is negative, f ( x ) has a relative
maximum.
Find inflection points of f (x ) algebraically.
Express f ′′( x ) as a fraction and set both numerator and
denominator equal to zero. Make sign chart of f ′′( x ) to
find where f ′′( x ) changes sign. (+ to – or – to +)
NOTE: be careful to confirm that f (x ) exists for any x-
values that make f “ ( x ) DNE.
Show that the line y = mx + b is tangent to
f ( x ) at ( x1 , y1 )
Two relationships are required: same slope and point of
intersection. Check that m = f ‘ ( x1 ) and that ( x1 , y1 ) is on both f (x ) and the tangent line.
Find any horizontal tangent line(s) to f ( x )
or a relation of x and y.
Write dy/dx as a fraction. Set the numerator equal to zero.
NOTE: be careful to confirm that any values are on the
curve. Equation of tangent line is y = b. May have to find b.
Find any vertical tangent line(s) to f ( x ) or a
relation of x and y.
Write dy/dx as a fraction. Set the denominator equal to zero.
NOTE: be careful to confirm that any values are on the
curve.
Equation of tangent line is x = a. May have to find a.
Approximate the value of f (0.1) by using
the tangent line to f at x = 0
Find the equation of the tangent line to f using
y − y1 = m( x − x1 ) where m = f ′(0 ) and the point
is (0, f (0 )) . Then plug in 0.1 into this line; be sure to use
an approximate (≈ ) sign.
Alternative linearization formula:
y = f ‘ ( a )( x − a ) + f ( a )
Find rates of change for volume problems.
Write the volume formula. Find dV/dt. Careful about product/chain rules. Watch positive (increasing measure)/negative (decreasing measure) signs for rates.
Find rates of change for Pythagorean
Theorem problems.
Find the average value of f (x ) on [a, b]
Find the average rate of change of f ( x ) on
[a, b]
f (b) − f ( a )/ b-a
Given v(t ) , find the total distance a particle travels on [a, b]
Given v(t ) , find the change in position a particle travels on [a, b]
Given v(t ) and initial position of a particle, find the position at t = a.
f (x )
f ( g ( x) ) g ‘( x)
Find area using left Riemann sums
A = base[x0 + x1 + x 2 + … + x n −1]
Note: sketch a number line to visualize
Find area using right Riemann sums
A = base[x1 + x 2 + x3 + … + x n]
Note: sketch a number line to visualize
Find area using midpoint rectangles
Typically done with a table of values. Be sure to use
only values that are given. If you are given 6 sets of
points, you can only do 3 midpoint rectangles.
Note: sketch a number line to visualize
Find area using trapezoids
Describe how you can tell if rectangle or
trapezoid approximations over- or under-
estimate area.
Overestimate area: LH for decreasing; RH for
increasing; and trapezoids for concave up
Underestimate area: LH for increasing; RH for
decreasing and trapezoids for concave down
DRAW A PICTURE with 2 shapes.
Given dy/dx, draw a slope field
Use the given points and plug them into dy/dx, drawing little lines with the indicated slopes at the points.
y is increasing proportionally to y
Solve the differential equation …
Separate the variables – x on one side, y on the other.
The dx and dy must all be upstairs. Integrate each side,
add C. Find C before solving for y,[unless ln y , then
solve for y first and find A]. When solving for y, choose
+ or – (not both), solution will be a continuous function
passing through the initial value.
Find the volume given a base bounded by
f ( x ) and g ( x ) with f (x ) > g ( x ) and
cross sections perpendicular to the x-axis are
squares
Given the value of F (a ) and F ‘ ( x ) = f ( x ) ,
find F (b )
The accumulation function: net (total if f ( x ) is positive)
amount of y-units for the function f ( x ) beginning at
x = a and ending at x = b.
Given v(t ) and s (0 ) , find the greatest
distance
from the origin of a particle on [a, b]
Solve v ( t ) = 0 OR DNE . Then integrate v(t ) adding
s (0 ) to find s (t ) . Finally, compare s(each candidate) and
s(each endpoint). Choose greatest distance (it might be
negative!)
Given a water tank with g gallons initially
being filled at the rate of F (t ) gallons/min
and emptied at the rate of E (t ) gallons/min
on [0, b] , find
a) the amount of water in the tank at m
minutes
b) the rate the water amount is changing
at m
c) the time when the water is at a
minimum
Find the volume of the area between f ( x ) and g ( x ) with f ( x ) \> g ( x ) , rotated about
the x-axis.
Given v(t ) and s (0 ) , find s (t )
Find the line x = c that divides the area under f ( x ) on [a, b] to two equal areas
Find the volume given a base bounded by
f ( x ) and g ( x ) with f (x ) > g ( x ) and
cross sections perpendicular to the x-axis are
semi-circles
