Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

population ecology > weeks 1-4 > Flashcards

weeks 1-4 Flashcards

1
Q

What is a population?

A
  • group of individuals of same species that live in the same place.
  • group of individuals that live close enough to find each other and reproduce.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is population ecology?

A
  • Study of how/why populations change over time and space, in terms of distribution, abundance and composition.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What’s the difference between a discrete and a continuous growth model?

A
  • Discrete models track time in discrete steps (1 year, etc.), while conituous models track growth over a continuous, smooth curve.
  • Discrete models use difference equations to model pop growth, while continuous models use differential equations.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What types of species are best-suited to discrete population growth models, and what types are best suited to continuous models?

A
  • DIscrete models: species with pulsed reproduction (seasonal repro) or species with non-overlapping generations (short-lived).
  • Continuous models: species with overlapping generations and non-seasonal reproduction.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

What’s the difference between a stable population and a stationary population?

What characteristic of the population are you describing with a stable population and what are you describing with a stationary population?

A
  • Stable populations have unchanging proportions of individuals in each demographic (i.e. adults vs. juveniles).
  • Stationary populations are not growing are declining (λ=1).
  • “Stable” described population distribution and “stationary” describes pop growth.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What’s the equation to predict population size at time (t) with a discrete population model?

A

Nt = λt * N0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

What is the equation for population growth using a continuous model?

A

dN/nt = rN, where r = b-d

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

What is the equation to determine pop size at time (t) using a continuous growth model?

A
  • Nt = No * ert, where r = b-d.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Derive equations to express λ in terms of r, and r in terms of λ.

A

Nt =λ t * No Nt = No * ert

So…

λ = er and r = ln (λ)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Derive the equation for doubling-time of a population using discrete growth.

A

Nt = λt * No

λt = Nt / No = 2

ln(λt) = ln(2)

t * ln(λ) = ln(2)

t = ln(2) / ln (λ)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

List 5 assumptions of an exponential growth model.

A
  1. b and d are constant over time.
  2. no differences in b and d by demographic group.
  3. no e or i.
  4. no time lags.
  5. no genetic structure.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Give 4 examples of populations that might be experiencing exponential growth.

A
  1. Newly established pops with few predators.
  2. Invasive species.
  3. Pops recovering from catastrophic declines.
  4. Humans.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Describe how stochastic models differ from deterministic models in terms of:

  1. predictability,
  2. outcomes and
  3. starting conditions.
A
  1. may vary unpredictably
  2. outcomes uncertain
  3. different starting conditions can produce different outcomes.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q
  1. What kind of pattern of population growth do deterministic factors create?
  2. Give 4 examples of deterministic factors.
A
  1. directional, non-random growth patterns.
  2. habitat loss
  3. fragmentation
  4. invasive species
  5. overharvest
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Name 3 primary sources of variation in population growth.

A
  1. Deterministic factors
  2. Sampling error
  3. Stochastic processes
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

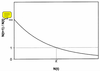
What is demographic stochasticity?

A

Chance variation in b and d in real populations (i.e. survival rate may be 0.726, but in any given year in a population of 10 individuals, you’re not going to have 7.26 survivors!) even when λ does not change.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

What is environmental stochasticity?

A

Uncertainty due to unpredictable changes in environmental stochasticity.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

What is the “funnel effect”?

A

Variance in N increases with time in a pop models with stochasticity.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

How do you calculate average growth rates in models with stochasticity?

Why?

A
  1. Use geometric mean (multiply the t growth rates and then take the t-th root.
  2. With no stochasticity, can just take average (arithmetic mean), but with stochasticity the arith mean will over estimate lambda.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Describe how you would use past year’s estimates of λ to model stochasticity.

What is an assumption of this approach?

A

Run many (say 1000) replicates, eac taking a value of λ at random from previous years’ data.

Assumes future variation will be same as past.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

What is the effect of temporal autocorrelation on stochastic population growth estimates?

A

Causes underestimation of variability in growth rates (b/c you measured for a few years, and those years tend to be more similar than others).

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q
  1. What is scramble competition?
  2. What’s another term for it?
A
  1. individuals have equal access to resources, so when shortages occur, everyone is equally affected.
  2. “exploitative competition”
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q
  1. What is contest competition?
  2. What is another name for it?
A
  1. Individuals have unequal access to resources, so those with less access suffer more when there are shortages.
  2. “interference competition”
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

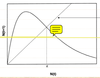
What is the logistic growth equation for density dependence?

A

dN/dt = rN (1-N/K)

where K is the carrying capacity

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

If a population is experiencing logistic growth, what is causing that?

A

Density-dependence.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

Graph r over N with exponential growth.

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

Graph N over time with exponential growth.

A
28
Q

Graph r over N with logistic growth.

A
29
Q

Graph N over time with logistic growth.

A
30
Q

Graph growth over population size with logistic growth.

A
31
Q

Graph growth over N with exponential growth.

A
32
Q

What is a theta-logistic model?

What is the equation?

A

Allows for non-linear relationship between pop growth rate and N.

dN/dt = rn [(1-N/K)Θ]

33
Q

What is Θ when there is a linear relationship between r and N?

A

Θ = 1

34
Q

What’s the equation for logistic growth where density-dependence occurs with at time lag?

A

dN/dt = r (1 - Nt-L/K)

35
Q

When density-dependence occurs with a time lag in pop with logistic growth, what do graphs of N over t look like when:

  1. rL is small
  2. rL is medium
  3. rL is large
A
  1. similar to logistic growth with no lag
  2. logistic growth with damped oscillations until K is reached.
  3. stable limit cycle (continous uniform period and amplitude oscillations) around K.
36
Q
  1. Graph Nt+1 over Nt for logistic growth with scramble competition.
  2. When will population increase and when will population decline?
A

Pop will grow to left of exact replacement line, decline to right of it.

37
Q

Graph Nt+1/Nt over Nt for logistic growth model with scramble competition.

A
38
Q

What is the discrete growth model equation for scramble competition?

What is this equation commonly called?

A

Nt+1 = Nt * λmax(1 - N/K)

“Ricker equation”

39
Q

What is the discrete growth model equation for contest competition?

What is this equation commonly called?

A

Nt+1 = Nt [(RmaxK) / (Rmax Nt - Nt + K)]

Beverton-Holt equation

40
Q

Recipe for chaos?

A
  • Scramble competition
  • Very larger growth rates (r > 2.7, λ > 15)
41
Q

What 3 things did Andrewartha and Birch propose as limits on population size?

Which is most important?

A
  1. shortage of resources
  2. inaccessability of resources
  3. shortage of time when r is positive (weather, predators, etc.)

Number 3 most important.

42
Q

What is density-vague population change?

A

Proposed by Don Strong as a more realistic (but less mathematically feasible) alternative to density dependence. At medium densities, that is not much change in growth rates relative to very high or very low densities.

43
Q

What 2 things might make you not notice density dependence in a population?

A
  1. Data sets with short time series!
  2. Time lags not taken into consideration.
44
Q

What might make you conclude there is density dependence, when there really isn’t?

A

Spurious correlations (like correlations between Nt+1/Nt vs. Nt).

45
Q

What are population dynamics?

A

Analyses of causes of changes in population density, including both population regulation (process that returns pop to its equilibrium density) and population limitation (process that sets equilibrium density).

46
Q

What is population regulation?

A

Mechanism that returns a population to its equilibrium density (as determined by population limitation).

47
Q

What is population limitation?

A

Process that sets the equilibrium density of a population (which occurs via mechanism of population regulation).

48
Q

How do you calculate reproductive value?

A

Repro value = # offspring an ind of a given age class will produce relative t the first age class (first age class always = 1.0).

49
Q

How do you calculate fecundity in a pre-breeding census?

A

Fx = mxSo

50
Q

What does the Leslie matrix look like for a pre-breeding census?

A
51
Q

How do you calculate fecundity in a post-breeding census?

A

Fx = Sxmx

52
Q

What does the Leslie matrix for a post-breeding census look like?

A
53
Q

What is a Lefkovitch matrix, and how does it differ from a Leslie matrix?

A

Just like a stage-structured Leslie matrix, but some individuals will stay in same stage, while others will move into next stage. So you get two survival values in the same row for each stage.

54
Q

What does a Lefkovitch matrix look like?

A
55
Q

Why do age and stage strucured models rarely include density dependence? (2 reasons)

A
  • It’s rare to know which parameters are affected, and how much, and by whom (is juv d-d only caused by # of other juv’s, or everyone?)
  • It’s a pain in the ass to calculate!
56
Q

How do you add demographic stochasticity to a stage-structured model?

A

Determine probability that each individual survives or reproduces using binomial (survival or repro of 1 offspring only) or Poisson (repro of > 1 offspring) distribution for each matrix element (vital rate).

57
Q

How do you add environmental stochasticity to stage-structured models?

A

Determine the mean and standard deviation of each matrix element from years worth of field data. Replicates of model are run with random samples within those standard deviations.

58
Q

What is sensitivity analysis?

A

Determines how sensitive pop growth is to changes in each vital rate in a matrix.

59
Q

How is sensitivity calculated?

A

Sensitivity = Δλ / Δv

where v = vital rate.

60
Q

The sensitivity of a matrix element depends on what 2 things?

A
  1. reproductive value of that age class.
  2. proportion of ind’s in that class at Stable Age Distribution.
61
Q

What is elasticity, and how does it differ from sensitivity?

A

Rescales sensitivity values to represent the proportional change in lambda due to the proportional change in the vital rate. (Allows you to compare percent differences when vital rates are not anywhere near equal.)

62
Q

How do you calculate elasticity?

A

Ev = (Δλ/λ) / (Δv/v)

where v = vital rate

63
Q

What are 2 assumptions of a cohort life table?

A
  1. No yearly variation in vital rates.
  2. Stable age distribution.
64
Q

What are 3 assumptions of a static life table?

A
  1. No yearly variation in vital rates.
  2. Stable age distribution.
  3. Stationary population.
65
Q

How is survivorship different from survival?

A

Survivorship is the probability of an ind in age group x living to a given age in a life table (not a matrix).

66
Q

Name 3 useful life-history values you can calculate from life tables.

A
  1. Net reproductive rate.
  2. Generation time
  3. Instantaneous rate of increase (r) (approximate)
67
Q

Name 4 key life-history tradeoffs.

A
  1. Current repro vs. survival.
  2. Current repro vs. future repro.
  3. Repro vs. condition/growth
  4. Number vs. quaity of offspring

population ecology (3 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions