Week2_Lab_Sampling_Distributions

Question 1

1. What is a sampling distribution?

Answer 1

MODEL ANSWER:

A (hypothetical) distribution of the values for a statistic obtained by computing the statistic in each one of a large number of samples.

A sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification en route to statistical inference. More specifically, they allow analytical considerations to be based on the sampling distribution of a statistic, rather than on the joint probability distribution of all the individual sample values.

Question 2

2. What is the name for the standard deviation of the sampling distribution for a statistic?

Answer 2

The standard deviation of this statistic is called the standard error.

The standard error (SE) is the standard deviation of the sampling distribution of a statistic, most commonly of the mean.

Question 3

3. How can you compute the S.D. of the sampling distribution of the mean, from statistics for a single sample?

Answer 3

MODEL ANSWER:

Take the sample S.D. and divide it by the square root of the sample size.

Other stuff..

The standard error (SE) is the standard deviation of the sampling distribution of a statistic, most commonly of the mean.

Step 1: Calculate the mean (Total of all samples divided by the number of samples).

Step 2: Calculate each measurement’s deviation from the mean (Mean minus the individual measurement).

Step 3: Square each deviation from mean. Squared negatives become positive.

Question 4

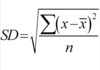
4. For a mean, if the data in the sample is normally distributed, what will be the shape of the sampling distribution of the mean?

Answer 4

Normal -

A bell curve - this will change depending on the sample n

Question 5

5. What shape is the sampling distribution for a z-statistic?

Answer 5

A bell curve with z = 0 in the middle going out to z = -2 and more..

Question 6

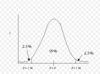
6. If the area under the standard normal curve is 100%, what percentage lies under the curve to the left of the line at z=-1.96?

Answer 6

2.5% 0r .025

Question 7

7. If the area under a standard normal curve is 100%, what % lies under the curve to the right of a line at z=1.65?

Answer 7

5% or .05

Question 8

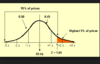
8. How does the shape of a t-statistic distribution differ from that of a z-statistic distribution?

Answer 8

It has flatter broader tails..

When n≥30, the sampling distribution of the sample mean becomes normal. If n≤30, the skewness of the population could influence the shape of the sampling distribution and make it not normal.

The t-statistic distribution may be lumpy from skewness due to low sample size