Week 9 Flashcards
What is a multivariate normal distribution?
A distribution for multiple variables
In Linear Mixed Models, why do we not JUST assume each random effect follows a normal distribution?
Because while it is true variables individually follow univariate distributions, multiple variables together sometimes follow a multivariate distribution.
It’s important to note variables together do not imply a multivariate distribution. But a multivariate distribution DOES imply univariate normal distribution.
What are the two basic parameters of a multivariate normal distribution?
The mean and variance
How do you calculate the variance?
Work out the Mean (the simple average of the numbers)
Then for each number: subtract the Mean and square the result (the squared difference).
Then work out the average of those squared differences.
Why is it important to get the variance before the SD?
Because in variance you get the mean (line of best fit) of all the data points, you then calculate the individual difference from each data point to the mean (the line of best fit), then with each individual diference you square each point, add together, and get the average again.
Once you have that overall number, the variance for the model, all you do to get the standard deviation is square it.
So you have to square the variance for the SD.
Why is getting the standard deviation useful in a model?
Because you can show which variables are within one Standard Deviation of the Mean. So, using the Standard Deviation we have a “standard” way of knowing what is normal, and what is extra large or extra small, for example.
In a multivariate normal distribution, how do the means and variances differ to in a univariate?
The means are a VECTOR of means, one for each variable, and the variances are in a q q covariance matrix.
What is a correlation coefficient?
Indicators of the strength of the linear relationship between two different variables, x and y.
When looking at a slope, what is this actually showing? And what are random slopes then?
The slope is the regression line (the mean of the data points across participants). It takes into account the mean and variance.
If the slope is random, we are allowing participants to have their differences taken into account. Because thes slope is the regression coefficient, it is capturing strength of the relationship between the variables, per participant. And that is done by assuming a mean (the fixed effect part) so that you have the average slope across people, then the SD (how much variability there is in the slope across people - so we allow their to be different varibaility)
In random slopes we can see the mean and SD, mean across people, and the SD. So allow for different varaibility
What makes up a random effect?
- the mean of the parameter across all partcipants (equivalent roughly to our familiar fixed effects)
- the Standard Deviation capturing how much the effect varies by person
If participants have a random intercept, but the same coefficient, what type of model is this?
This would look like one regression line (one slope) but different intercepts.
This is a random intercept fixed effect model.
For random effects and random intercepts, why do we have a standar deviation for them
Capturing how much that random effect varies by person.
What is Mahalanobis distance?
Difference between variance and covariance?
Variance is how much one variable varies within the sample, or population.
Co variance is how much TWO or more variables vary together.
How is correlation and covariance related?
With correlation you will find out the strength and direction of the change in X equalling the change in Y.
So not just as X increases so does Y. But HOW aligned are those data points with the line of best fit - are they close? If so, strong.
However, covariance just show the DIRECTIOn of the association. As X goes up, Y goes up. It’s talking about how the change happens together, not the strength.
So covariance for Eugene and Diana is as Eugene goes left Diana goes right. Direction.
The correlation for Eugene and Diana, how strongly they relate together, is different. Correlation shows not only does as Eugene goes left Diana goes wright, but their relationship (strength) is also a negative weak one, as indicated by how far the data points are from regression line.
so is that just variance? no co variance because looking at how much two or more variables bary together.
Variance is just how much one variable varies within the sample.
What is this showing?
Other than being an equation for a random intercept only model
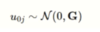
u0j = individual unit deviations from the mean intercept
G =. model is normally distributed between 0 and the SD of the deviations.
