Week 8 Game Theory

Question 1

Explain a ‘Game’ and name all the necessary parts of it.

Answer 1

Question 2

Illustrate the ‘Prisoner’s Dilemma’.

Answer 2

Question 3

Define Parteto Efficency.

Answer 3

We are in a pareto efficient situation, if it is impossible to make one agent better off without making any agent worse off.

e.g. Prisoner’s Dilemma is not pareto efficient.

Question 4

Define a Strictly Dominant Strategy.

Answer 4

A Strictly Dominant Strategy is always the best strategy (highest payoff), independently of what the other player chooses to do.

Question 5

Define a Strictly Dominated Strategy.

Answer 5

A strategy is Strictly Dominated if there exists another strategy that guarantees a strictly higher payoff, independently of what the other player chooses to do.

Question 6

Define the assumption of Common Knowledge.

Answer 6

The assumption of Common Knowledge states that every player knows everything (strategies & payoffs) about the game.

Question 7

Define a Nash Equilibrium.

Answer 7

A NE is a profile of strategies for all players, s.t. the strategy played by each player guarantees the highest payoff, given what the other player are doing.

Question 8

Calculate the mixed strategy NE in the Aikman’s / Keys game.

(Assume two players with the payoff (2,1) for Aikman’s and the payoff (1,2) for Keys.)

Answer 8

Question 9

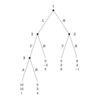
Show a subgame on a game tree.

Answer 9

Question 10

Compute the Subgame Perfect Nash Equilibrium/a of the game.

Answer 10