Week 4

Question 1

What S-shape adoption? How can it be recognized?

Answer 1

Question 2

What is the Bass-model? What are its parameters? And its formulas?

Answer 2

Question 3

What are some useful features of the Bass model? What are its requirements?

Answer 3

Question 4

When do we care about the size of the giant component in a Poisson random network? And why do we care?

Answer 4

Question 5

How do we calculate the size of the giant component q (in this case for a Poisson random network)? How is this derived?

Answer 5

(see image)

Note: that we thus need to solve for - log(1 - q)/q = (n - 1)p (i.e. = E[d])

Question 6

What is the probability of being in the giant component?

Answer 6

Question 7

What is the SIS-model? What does it consist of?

Answer 7

Question 8

When is the SIS model in steady state?

Answer 8

(see image)

If we drop 𝜀 we get 𝜌 = 1 - 𝛅/v

Question 9

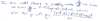
When will infections drop and eventually be disappear in the SIS model?

Answer 9

Question 10

How can we introduce networks in the SIS model?

Answer 10

Question 11

How can we derive the steady state in the SIS model with a network?

Answer 11

Question 12

How can we find the steady state in the SIS model in a Regular and Scale Free network?

Answer 12