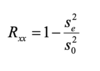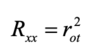Week 3 - 4: Reliability Flashcards
The reliability coefficient varies between
0 and 1
Reliability refers to
the consistency of a measuring tool
Is reliability all-or-nothing or on a continuum?
Continuum. That is, a measuring tool or test will be more or less reliable
Two components that CTT assumes are present in an observed score
true score + measurement error
True score
the actual amount of the psychological characteristic being measured by a test that a respondent possesses.
Measurement error
the component of the observed score that does not have to do with the psychological characteristic being measured
According to CTT, reliability is the extent to which differences in respondents’ ______ scores are attributable to differences in their_________ scores, as opposed to __________ ___________
observed, true, measurement error
3 sources of measurement error
- Test construction 2. Test administration 3. Test scoring and interpretation
Examples of sources of measurement error in Test construction
• item sampling (variation among items in a test) • content sampling (variation among items between tests)
Example of sources of measurement error in test administration
• test environment (temperature, lighting, noise) • events of the day (positive vs. negative events) • test-taker variables (physical discomfort, lack of sleep) • examiner-related variables (physical appearance & demeanour)
Example of sources of measurement error in Test scoring and interpretation
• subjectivity in scoring (grey area responses) • recording errors (technical glitches)
Reliability depends on two things:
- The extent to which differences in test scores can be attributed to real individual differences 2. The extent to which differences in test scores are due to error expressed as: Xo = Xt + Xe
2 key assumptions of CTT
- Observed scores on a psychological measure are determined by a respondent’s true scores plus measurement error 2. Measurement error is random—it is just as likely to inflate a score as to deflate it -error tends to cancel itself out across respondents -error scores are uncorrelated with true scores
A reliability coefficient acceptable for research purposes
.7 or .8
A reliability coefficient needed for applied purposes
.9
Tau Equivalence
participants true scores for one test must be exactly equal to their true scores on the other test
Parallel tests must satisfy the assumptions of CTT as well as further assumptions which are
- participants true scores for one test must be exactly equal to their true scores on the other test—known as “tau equivalence” 2. the tests must have the same level of error variance
standard deviation of error scores tell us in “test score units” the…
the average size of error scores we can expect to find when a test is administered to a group of people
The standard deviation of error is also known as
the standard error of measurement
the correlation between parallel test scores is equal to
the reliability
Thus, parallel forms of a test exist when, for each form, the observed scored means and variances are
the same
Different content problem
Two forms of a test may meet the requirements of CTT, but not measure the same psychological attribute because they posses different content
carryover effects examples
For example, a respondent’s memory for test content, attitudes, or mood state might similarly affect performance on both forms of a test
According to CTT error scores on one form of a test should be ______________ with error scores on a second form of a test
uncorrelated
4 assumptions of CTT and parallel tests
the observed scores on each form are the sum of the true scores and error scores • the true scores are the same for the two forms • the error scores for each form sum to 0 and have the same variance • true scores are uncorrelated with error scores
How is test-retest reliability estimated
by correlating respondents test-retest scores
The test-retest method depends on the same assumptions as the alternate forms method, these are (2):
1 people’s true scores should not change between the two testing occasions 2 the error variances of the two tests should be identical • The observed test-retest scores should therefore have the same means and variances
3 threats to the “true score stability” assumption
1 construct instability 2 length of test-retest interval 3 developmental changes
test-retest correlation is sometimes known as
the coefficient of stability
If the true scores change during the test-retest interval, then the reliability coefficient will reflect two factors:
1 the degree of measurement error 2 the amount of change in true scores
two factors that determine the internal consistency reliability of test scores:
1 The consistency among parts of a test: • if the test items are strongly correlated with each other, the test is likely to be reliable 2 The test’s length: • all things being equal, a longer test will be more reliable than a shorter test
r four methods of estimating internal consistency
1 Split-Half Reliability 2 Coefficient α 3 Standardised Coefficient α 4 KR-20
three steps to computing the split-half reliability
1 Divide the test into equal halves 2 Calculate the correlation between scores on the two halves of the test 3 Adjust the half-test reliability using the Spearman-Brown formula
Variance Covariance Matrix - The diagonal elements
The diagonal elements in the matrix are the “item variances”
Variance Covariance Matrix -The off-diagonal elements
The off-diagonal elements in the matrix are the “inter-item covariances” (the associations between each item and every other item, as measured by covariance)
coefficient α typically ranges in value from
0 to 1
Coefficient α assumptions
1.The α method assumes that test items are essentially tau equivalent • each item is an equally strong indicator of the true score scores, but they may differ in their precision by a constant ( in other words, the items can have different means) 2 Items can have possibly different error variances 3 Error scores should be uncorrelated with true scores—error should be random (assumption for all forms or reliability 4 Coefficient α assumes that all items used to generate a composite score measure the same attribute or construct
What level of α may be “too high” and indicate redundancy in the items
.9 or greater
does coefficient α measure “unidimensionality”?
no
What formula for internal consistency was made for determining the internal consistency reliability of composite scores based on dichotomously scored items
KR-2-, however cronbachs a works too
why is a long test is more reliable than a short test
Increasing the length of a test by adding new items that measure the same construct as the original items will increase the true score variance more than the error variance
All types of reliability are estimated:
quanitatively
Reliability is a property of:
scores, not a test. Strictly speaking, a test is not found to be reliable.
True score:
A true score is a hypothetical score devoid of measurement error.
Observed Score:
Observed scores are the scores we obtain from tests or instruments.
The discrepancy between observed scores and true scores is considered to be due to
measurement error.
Error Scores assumptions:
Error scores should have a mean of zero. Error scores should be a random process Error scores should be uncorrelated with true scores
Four ways to think about reliability:
- The ratio of true score variance to observed score variance 2. Reliability as a lack of error vairance 3. Reliability as the (squared) correlation between observed scores and true scores 4. Reliability as the lack of (squared) correlation between observed scores and error scores.
Interpretation guidelines for reliability: Unnacceptably low: Minimum for beginning stage research: Good level for research purposes: Necessary for important decisions:
.60 .70 .80 .90
The ratio of true score variance to observed score variance
This conceptualisation is similar to eta squared: the ratio of SSEffect to SSTotal
Conceptually, in the reliability case, it is the ratio of SSTrue to SSObserved
- Reliability as a lack of error variance
Instead of the ratio of true score variance to observed variance, in this case we speak of the ratio of error variance to observed variance.
We subtract this ratio by 1 to place in the same context of reliability (rather than error).
- Reliability as the (squared) correlation between observed scores and true scores
- Reliability as the lack of (squared) correlation between observed scores and error scores.
If reliability is the correlation between true scores and observed scores, then it is necessarily the case that it is the relative absence of a correlation between observed scores and error scores.
Parallel Tests
Essentially, two tests are considered parallel if they are identical to each other psychometrically, but differ in the actual items that make up each test.
All tau-equivalence assumptions:
Tau-equivalence, in this context, implies that the true scores associated with each test represent the same construct.
Thus, a person’s true score on one test would be expected to be identical on the other test.
Plus, assumes equal error variances between the two tests, as well.
According to CTT, the correlation between the composite scores on Test 1 and the composite scores on Test 2:
represent the reliability associated with the scores. Thus, the closer the correlation is to 1.0 the more reliable we consider the scores to be. If the correlation is very high, it is telling us that the test scores represent “something” in a very precise way.
Two sources of information can help us evaluate an individual’s test score
1 a point estimate: a “best estimate” of a person’s true score
2 a confidence interval: the range in which the true score is likely to fall
Point estimates and confidence intervals are directly affected by the test score ______________ ________________
reliability coefficient
two kinds of point estimates of a person’s true score that can be computed from a person’s observed score:
1 An individual’s observed test score
2 An adjusted true score estimate
A point estimate based solely on a person’s observed score on a test fails to account for
measurement error
The second point estimate—known as an adjusted true score estimate—takes such measurement error into account
The adjusted true score estimate reflects an effect called
regression to the mean
The adjusted score estimate reflects the discrepancy in an individual’s observed score that is likely to arise between two testing occasions. The size and direction of this discrepancy is a function of three factors:
1 the size of the reliability coefficient
• Poor reliability produces bigger discrepancies between the estimated true score and the observed score
2 the size of the difference between an individual’s observed test score and the mean
• The difference between the estimated true score and the observed score will be larger for relatively extreme observed scores (high or low) than for relatively moderate scores
3 the direction of the difference between an individual’s observed test score and the mean (whether the score was above or below the mean)
The adjusted score estimate is the best estimate of
a predicted true score
Confidence intervals reflect
the precision of the point estimate of an individual’s true score
Point estimates of an individual’s true score are usually reported with
true score confidence intervals
Confidence intervals are constructed using the
standard error of measurement
The sem is the __________ ______________ of a theoretically normal distribution of test scores obtained by one person on equivalent tests
standard deviation
In accordance with CTT, an observed test score is one point in the theoretical _________ of ____________ the test-taker could have obtained
distribution, scores
The sem allows us to estimate, with a specific level of confidence (typically 95%),….
the range in which the true score is likely to exist
To use the sem to estimate the confidence interval of the true score, we make an assumption
If the individual were to take a large number of equivalent tests, scores on those tests would tend to be normally distributed, with the individual’s true score as the mean
Since the sem functions like a standard deviation in this context, we can use it to predict what would happen if an individual took additional equivalent tests
Approximately _______ of the scores would be expected to occur within ±1sem of the true score
68%
Approximately _____ of the scores would be expected to occur within ±2sem of the true score
95%
Approximately _____ of the scores would be expected to occur within ±3sem of the true score
99%
Suppose an individual obtained a score of 50 on one spelling test and that test had a sem of 4, then using 50 as the point estimate we can be 68% (±1sem) confident that the true score falls between
46 and 54
95% confidence interval formula
95% CI = Xo ± (z95%)(sem)
z95% is the z score from a normal distribution table corresponding to a score below which 95% of the area of the normal distribution, this equals to
1.96
z68% =
1
z75% =
1.15
z85% =
1.44
Highly reliable tests will produce________confidence intervals than less reliable tests
narrower
According to CTT, the correlation between the observed scores on two measures (rxo yo ) is determined by two things:
1 the correlation between the true scores on the two psychological constructs being assessed by the measures (rxt yt ) and 2
the reliabilities of the two measures (Rxx, Ryy)
observed associations (i.e., between measures) will always be weaker than true associations because
of measurement error
it is possible to estimate the true association between a pair of constructs by employing a formula known as
the correction for attenuation
