Week 1: Factors affecting Flow through Tubes

Question 1

Define pressure

Answer 1

Pressure is the force supplied per unit area

Question 2

Define pressure gradient

Answer 2

Pressure gradient is the difference in forces applied (per unit area) across ends of a tube/ either side of a membrane.

Question 3

Define Resistance

Answer 3

Resistance is the force that tends to oppose flow.

Question 4

Define Flow

Answer 4

Flow is the volume of liquid that passes through the circulation/respiratory system per unit time. Normally given in ml/second or L/min.

Question 5

How does pressure change across the vascular tree? What does this mean for the storage of blood volume?

Answer 5

Arteries tend to carry blood at higher pressure (100 mmHg). This pressure declines from arteries to muscular arteries- distributing arteries- arterioles- capillary- venules- veins (0-8mmHg). This means veins tend to hold blood- capacitance vessels holding 67% systemic blood. Compared to only 5% in capillaries and 11% in arteries.

Question 6

What is flow at any level of the circulation?

Answer 6

Cardiac output is 5L/min therefore flow of blood is 5L/ min at any level of the circulation.

Question 7

How is flow of fluid (fluid being either blood or air) generated in a) the systemic circulation b) the respiratory system

Answer 7

In the systemic circulation flow of blood is generated by a central pump that is able to pump at sufficient force to overcome systemic resistance. In the respiratory system flow of air is dependent on pressure gradients described by Boyle’s law: P = 1/ volume Pressure is inversely proportional to volume. Therefore when we inspire we increase the volume of our thoracic cage, pull on the pleura which expands outwards, the pressure within the lungs drops due to expanded volume and atmospheric pressure is above that of thoracic –> air moves in. Expiration opposite: compress thoracic volume, pressure rises, air is expelled.

Question 8

What force generates flow?

Answer 8

Blood flow is generated by a pressure gradient across the vascular tree/ respiratory system. Flow is directly proportional to the pressure gradient between ends of vessels/ airways I.e double pressure gradient, double the flow. Flow (Q) ∝ pressure gradient (△P)

Question 9

For a given pressure gradient, what is flow affected by/ inversely proportional to? What is the overall equation for flow?

Answer 9

Flow is inversely proportional to resistance of the airway/ blood vessel

Flow (Q) = Pressure gradient (△P) / Resistance (R)

Question 10

What is resistance dependent on? If we increased resistance what could restore flow?

Answer 10

Resistance is dependent on the radius of the vessel/ airway. If we increase resistance we can restore flow by increasing the pressure gradient.

Question 11

What clinical equation is there that mimics △P = Q x R

Answer 11

The equation for blood pressure:

BP = CO x SVR

Blood pressure = cardiac output x systemic vascular resistance

Question 12

Define velocity

Answer 12

Velocity is the rate of movement of fluid particles along a vessel/ airway measured in cm/ second.

Question 13

What is velocity directly proportional to/ inversely proportional to?

What is the equation for velocity?

At a constant flow, how does velocity change with altering the vessel radius?

Why is a narrowed vessel/ decreased radius clinically important?

Answer 13

Velocity is directly proportional to flow over the cross sectional area of the vessel.

V= Q / A

where V = velocity Q= Flow A = Cross sectional Area (π r2)

Increasing or decreasing the vessel radius at a constant flow (e.g. CO = 5L/min) alters the velocity of fluid movement.

At constant flow: Increasing the cross sectional area of the vessel decreases velocity

Decreasing the cross sectional area increases velocity of fluid movement.

This is clinically important as narrowing of vessels at constant flow leads to increased velocity and turbulent flow.

Question 14

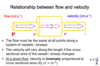
What type of flow is normally seen throughout vessels/ tubes of the body?

Describe this type of flow.

When the pressure gradient is constant (not flow) what happens when you alter the vessel radius to:

1) flow itself
2) velocity of flow

So at a constant pressure gradient what is mean velocity directly proportional to?

Answer 14

• Laminar flow is normally seen throughout vessels/ tubes of the body. Laminar flow forms a parabolic curve with the highest velocity of flow in the centre of the vessel, which slows as you approach the vessel edges. (almost stationary at vessel edge).
• At a constant pressure gradient flow will be entirely dependent on the resistance of the vessel which is determined by the vessel radius. (Q= △P/ R when R inversely proportional to radius)
• If the vessel radius is decreased the resistance will increase which in turn decreases flow.
• If vessel radius is decreased this also means there is less time for laminar flow to build its velocity, meaning the mean velocity of flow is also reduced.
• At a constant pressure gradient mean velocity of flow is directly proportional to the radius squared.

Question 15

What three things determine resistance to flow?

What is the equation for resistance that takes into account these three factors?

Answer 15

1. Length of the vessel
2. Viscosity of the fluid
3. Vessel radius

Resistance= 8 x n x l / π r4

Question 16

What is poiseulle’s law?

State the equation

What does this mean if the radius of a vessel is doubled/ halved?

Answer 16

Poiseulle’s law states that flow is proportional to the pressure gradient x radius of the vessel to the power of 4 over 8 x length of the vessel x viscosity of the fluid.

Q= △P x π r4 / 8nl

This means flow is directly proportional to the radius to the power of 4 (π r4).

Therefore if radius is doubled, flow will increase by a factor of 16. (2 to power of 4).

If radius is halved, flow will decrease by a factor of 16.

Question 17

Under normal physiological conditions, blood pressure tries to maintain a constant flow.

What needs to alter when the radius of a vessel is narrowed to maintain constant flow?

What effect does narrowing the vessel radius have on mean velocity when flow is constant?

Answer 17

• When the radius of a vessel is narrowed, the pressure gradient needs to increase to maintain a constant flow as per Poiseulle’s law:

Q= △P x π r4 / 8nl

• To maintain Q, when 8nl= constant and π r4 has decreased, △P needs to increase. If radius is halved, △P needs to increase by a factor of 16.
• Mean velocity will increase when the vessel radius is narrowed to ensure the same flow.

Question 18

For constant flow, seen that when the vessel radius halves the pressure gradient has to rise by a factor of 16 and velocity rises by 4.

For constant pressure gradient consider what happens to the flow and velocity when the radius of the vessel halves?

Answer 18

• At constant pressure gradient, but not constant flow:
  
  • When vessel diameter halves the resistance to flow increases (Q= △P/ R) (R= 8nl/ π r4) meaning flow decreases by a factor of 16
  • The velocity of flow decreases by a factor of 4.

Question 19

What are three clinical applications of poiseulle’s law?

Answer 19

• Remember poiseulle’s law and the relationship between vessel diameter and flow is important for:
• Iv cannulas
• Endotracheal tubes
• Disease states which reduce the diameter of a vessel e.g. atherosclerotic plaque

Question 20

How is blood viscosity determined?

In laminar flow, where are blood cells vs plasma?

Answer 20

• The viscosity of blood is affected by the cellular component of blood
• Increased cellular component would increase blood viscosity (e.g. high altitude, increase RBC content of the blood).
• In laminar flow blood cells tend to be pushed centrally into the fast stream of laminar flow, whereas plasma tends to moved to the outside.

Question 21

What is turbulent flow?

What conditions can increase the likelihood of laminar flow?

Answer 21

• turbulent flow occurs when blood laminae become broken up, leading to disordered movement of blood cells throughout the blood vessel.
• Three factors increase the likelihood of turbulent flow:
  
  • High velocity of blood flow
  • Low viscosity of blood (layers easily break apart)
  • Large diameter of the vessel (without concurrent change in velocity of flow, especially at large artery branch points).
  • However remember that velocity increases as vessel diameter decreases, therefore vessel narrowing can increase the likelihood of turbulent flow.

Question 22

Turbulent flow is ______ - it will give rise to sounds/ murmurs:

_______ in arteries

________ in airways

In turbulent flow ________ to flow is increased.

Turbulent flow results in damage to __________.

Answer 22

Turbulent flow is NOISY giving rise to sounds/ murmurs:

BRUITS in arteries

WHEEZE in airways

In turbulent flow RESISTANCE to flow is increased.

Turbulent flow results in damage to the ENDOTHELIUM.

Question 23

Given than resistance increases as the radius of a vessel decreases, what is the expectation for small vessels? why is the resistance of the capillaries not much more than the aorta?

What vessels have the highest resistance in the circulation?

Answer 23

The expectation is that smaller vessels will have a higher resistance than larger ones. For individual vessels this is true, however in the total circulation capillaries dont have a much higher resistance than the aorta as the vessels are in parallel- providing many routes for blood to travel through.

The highest resistance vessels are the arterioles.

Question 24

Describe the effect of branching the circulation on the resistance?

What equation determines the resistance of vessels in series?

Answer 24

• For vessels that are in series, the resistance to flow is additive: r1 + r2 = R
• Branching the circulation reduces the overall resistance as there are more routes for blood to travel through. Flow is inversely proportional to the resistance which is determined by:

r1 x r2 / r1 + r2

Question 25

how does pressure change as blood flows through the circulation and encounters more resistance to flow?

Answer 25

The pressure within the vessels drops as the blood flow travels through the vessels encountering increasing resistance.

Question 26

What is transmural pressure?

What is the equation for transmural pressure of vessels?

What does high intravascular pressure tend to do?

What would happen if intravascular pressure were zero?

Answer 26

• Transmural pressure is the difference in the pressures applied across a wall (vessel wall)
• Transmural P for vessels = intravascular pressure - extravascular pressure
• High intravascular pressure tends to push open the vessel, reducing resistance to flow
• Therefore there is the tendency for resistance to fall as intravascular pressure increases
• If intravascular pressure were zero this would collapse the vessel and occlude blood flow.

Question 27

Describe how resistance changes with a rigid tube vs a distensible tube?

What property do blood vessels have which is important for flow? What other property does this first property give blood vessels?

What type of vessel is especially known to have this second property? What proportion of blood is stored in these types of vessels?

Answer 27

• With a rigid tube resistance is constant, therefore increasing intravascular pressure will increase flow but as a linear relationship.
• With a distensible tube, higher intravascular pressure opens the vessel which reduces resistance, meaning flow increases with a curved relationship.
• Blood vessels are distensible this is key to flow.
• The distensibility of blood vessels gives them CAPACITANCE.
• Veins are especially compliant and thereform have high capacitance- are known as capacitance vessels.
• Veins store 67% of systemic blood.