Week 1

Question 1

Undirected Network:

Answer 1

A node in the ajacency matrix takes value 1 (g_ij=1)

iff

i & j are linked undirected

the ajacency matrix must be symmetric.

Question 2

Directed Network

Answer 2

Links originate at one node and end at another, does not need to be symmetrical.

g = { 12, 14, 24, 41,43 }

or

g = { 12, 14, 24, 41,43 }
order of pairs matters

Question 3

Weighted Directed
Network (1/2)

``row stochastic’’

Answer 3

There are probablities [0,1] associated with the presence of a link rather than a binary 1 or 0.

Question 4

Weighted Directed
Network (2/2)

Answer 4

Question 5

What is the notation for Nodes, vertices, or players?

Answer 5

N={1,…,n}

Question 6

Representations of the ajacency matrix?

Answer 6

g in {0,1} ^n×n

(unweighted, possibly directed)

Question 7

What does the notation g_ij = 1 typically indicate?

Answer 7

indicates a link, tie, or edge between i and j in the ajacency matrix

Question 8

What is a path?

Answer 8

Path: a walk (i₁ ,i ₂ ,… i _K ) with each node i_k distinct

A path doesn’t go through the same node twice.

Question 9

What is a cycle?

Answer 9

Cycle: a walk where i ₁ = i _K

Nodes are not ordered, it is arbitrary since the walk ‘returns’ to the same node over again.

Question 10

What is the definition of Geodesic?

Answer 10

a shortest path between two nodes

Question 11

Define a walk

Answer 11

A Walk from i ₁ to i _K is a sequence of nodes (i₁,i₂ ,…, i_K )
and sequence of links (i₁ i₂ ,i₂i ₃ ,…,i_K‐1 i_K ) such that
i_k‐1 i_k in g (ajacency matrix) for each k.

Convenient to represent it as the corresponding
sequence of nodes (i ₁ ,i ₂ ,…, i _K ) such that i _k‐1 i _k in the ajacency matix (g)
for each k

Question 12

Describe the Paths, Walks, Cycles…

Answer 12

Path (and a walk) from 1 to 7:
1, 2, 3, 4, 5, 6, 7

Question 13

Describe the Paths, Walks, Cycles…

Answer 13

Walk from 1 to 7 that is not a path:
1, 2, 3, 4, 5, 3, 7

Question 14

Describe the Paths, Walks, Cycles…

Answer 14

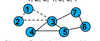
Simple Cycle (and a walk)
from 1 to 1: 1, 2, 3, 1

Question 15

Describe the Paths, Walks, Cycles…

Answer 15

Cycle (and a walk) from 1 to 1:
1, 2, 3, 4, 5, 3, 1

Question 16

What useful information do we get from raising g to the nth power?

Answer 16

gⁿ is a useful way to calculate the number of walks of length n

Question 17

(N,g) is connected if…?

Answer 17

(N,g) is connected if there is a path between
every two nodes

Question 18

What is a component?

Answer 18

Component: maximal connected subgraph
– (N’,g’) is a subset of (N,g)
– (N’,g’) is connected
– i in N’ and ij in g implies j in N’ and ij in g’

Imagine a bunch of nodes, they are connected in little subgroups that are detached from other subgrouns. The subgroups are components.

All of the nodes are needed to get a network (N,g)

Question 19

What is diameter of a network?

Answer 19

Diameter – largest geodesic (largest shortest path)
– if unconnected, of largest component…