Visualization and Exploration Flashcards
Unstructured data (tree)
Investigating individual features
Continuous features
Feature
Count
% Miss
Card
Min
1st Qrt
Mean
Median
3rd Qrt
Max
Std Dev
Investigating individual feature
Categorical Features
Feature
Count
% Miss
Card Mode Freq
Mode %
2nd Mode
2nd Mode Freq
2nd Mode %
Investigating individual features
Feature
Count
% Miss
Card
1st Qrt
Mean
Median
3rd Qrt
Max
Std Dev
Investigating individual features
Feature
Count - number of instances
% Miss - percentage missing
Card - cardinality: number of unique values
Min - minimum
1st Qrt
Mean - mean
Median - median (middle value)
3rd Qrt
Max - maximum
Std Dev - standard deviation
Investigation individual features
Categorical Features
Feature
Count
% Miss
Card
Mode
Mode Freq
Mode %
2nd Mode
2nd Mode Freq
2nd Mode %
Investigation individual features
Categorical Features
Feature
Count - number of instances
% Miss - percentage missing
Card - cardinality. number of unique values
Mode - mode: most common value
Mode Freq - frequency of mode
Mode % - percentage of mode
2nd Mode
2nd Mode Freq . similiar values for second most common value
2nd Mode %
Different types of histograms
Uniform
Normal (Unimodal)
Unimodal (skewed left/right)
Exponential
Multimodal
Uniform
Normal (Unimodal)
Unimodal (skewed left/right)
Exponential
Multimodal (more than one peak)
Normal distribution (68-95-99.7)
In statistics, the 68–95–99.7 rule, also known as the empirical rule, is a shorthand used to remember the percentage of values that lie within an interval estimate in a normal distribution: 68%, 95%, and 99.7% of the values lie within one, two, and three standard deviations of the mean, respectively.
Six sigma
rocesses that operate with “six sigma quality” are assumed to have less than 3.4 defects per million cases. This is based on six sigma with a “drift” of +/- 1.5 sigma.
Data quality - ypical problems
• Data may be …
- incomplete (missing instances/attributes),
- invalid (impossible values),
- inconsistent (conflicting values),
- imprecise (approximated or rounded), and/or
- outdated (based on old observations)
Missing values handling
4 options
- Feature is missing for some instances.
- Options:
- Remove feature completely.
- Only consider instances that have a value (per
feature). - Remove all instances that have one of the features
missing. - Repair missing features (imputation)
Impossible values
Can be handled like missing values.
Unlikely values
• Dates: One may expect a uniform distribution over months
and days.
− When formats DD-MM-YYYY and MM-DD-YYYY are mixed
up this is no longer the case.
− Days 1-12 are more frequent than 13-31
- Age: An age of 123 is not impossible, but unlikely.
- Price: An item priced 120.000 (rather than 120).
- Unlikely values are identified based on domain knowledge.
- Outlier values are identified based on the distribution.
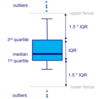
Box plots
• Median value (middle) depicted
by “Bar”
• IQR = Interquartile Range
(covers 50% of “middle”
instances) depicted by “Box”.
• Upper whisker: maximal value
below 3rd quartile + 1.5 * IQR.
• Lower whisker: minimal value
above 1st quartile - 1.5 * IQR.
• Outliers are drawn separately.
• Median value (middle) depicted
by “Bar”
• IQR = Interquartile Range
(covers 50% of “middle”
instances) depicted by “Box”.
• Upper whisker: maximal value
below 3rd quartile + 1.5 * IQR.
• Lower whisker: minimal value
above 1st quartile - 1.5 * IQR.
• Outliers are drawn separately.
Handling outliers with Boxplots
- Remove values above and below thresholds (e.g.,
upper and lower fences). - Clamp values above and below thresholds to these
thresholds.
Some basic descriptive statistics
sample mean formula
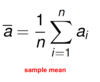
Soma basic descriptive statistics
sample variance
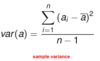
Some basic descriptive statistics
Sample covariance
Correlation
Normalization typically maps values
onto a predefined range (e.g. [0,1], [-1,1])
while maintaining relative differences.
Standard score uses the standard deviation to normalize.
