Unit Circle Flashcards
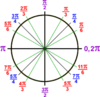
Locate the following:
π
π/2
2π
3π/2
0
π = 180°
π/2 = 90°
3π/2 = 270°
2π = 360° = 0°
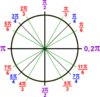
Locate the following:
π/3
π/4
π/6
π/3 = 60°
π/4 = 45°
π/6 = 30°
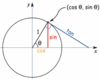
On the unit circle the x and y coordinates are found by?
cosØ = x
sinØ = y
The cartesion form of the unit circle is:
x² + y² = 1
what is the equivalent parametric form?
cos²Ø + sin²Ø = 1
cosØ =
sinØ =
tanØ =
x
y
sin/cos
What are the reciprocal functions of:
cosØ
sinØ
tanØ
1/cosØ = secØ
1/sinØ = cosecØ
1/tanØ = cotØ
The parametric equation for unit circle is:
cos²Ø + sin²Ø = 1
Divide this by cos²Ø:
1 + tan²Ø = sec²Ø
The parametric equation for unit circle is:
cos²Ø + sin²Ø = 1
Divide this by sin²Ø:
cot²Ø + 1 = cosec²Ø
Complete the following:
cosØ =
secØ =
sinØ =
cosecØ =
tanØ =
cotØ =
cosØ = x
secØ = 1/cos
sinØ = y
cosecØ = 1/sin
tanØ = sin/cos
cotØ =cos/sin
What is meant by the periodic property of sin and cos?
cosØ = cos(Ø + 2kπ)
sinØ = sin(Ø + 2kπ)
*π = 180°, therefore 2π = 360°
so any multiple of 2π will result in the same position on the circle.
e.g. Ø + 2kπ, Ø = 90, k =3
90 + 2(3)180
90+ 1080
90 + 3(360)
e.g start at 90 and go around 3 full circles. You end up where you started, at 90.
CAST divides the unit circle into 4 quadrants.
Which quadrant do the following belong to?
π - Ø
π + Ø
2π - Ø
π - Ø = 2nd
π + Ø = 3rd
2π - Ø = 4th
In which quadrant is:
tan positive?
cos positive?
sin positive?
secØ =
cosecØ =
cotØ =
1/cos
1/sin
cos/sin
sin(-Ø) =
cos(-Ø) =
sin(-Ø) = -sin(Ø)
cos(-Ø) = -cos(Ø)
Can you explain why?
sin(-Ø) = -sin(Ø)
cos(-Ø) = -cos(Ø)
Can you explain why?
sin(x) is an odd function (symmetrical about the origin) - therefore f(x) = -f(x)
cos(x) is an even function (symmetrical about the y-axis).
