Unit 4: Probability

Question 1

Geometric Probability

Answer 1

Looking for “the first” success in n trials.

Question 2

Binomial Probability

Answer 2

Looking for “x” number of success in n trials.

Question 3

Random Variable

Answer 3

Variable that quantifies a set of outcomes

Question 4

Model for a Discrete Random Variable

Answer 4

Table in which outcomes are on the top row and corresponding probabilities are on the second row

Question 5

Distribution for a Discrete Random Variable

Answer 5

Histogram that shows the outcomes on the x-axis and probabilities on the y-axis.

Question 6

Expected Value

Answer 6

Mean of a Random Variable. Sum of the product of outcomes and probabilities.

Question 7

Independent Events

Answer 7

P(A and B) = P(A)×P(B)

Question 8

Tree Diagram

Answer 8

Use when two events are dependent.

Question 9

10% Condition

Answer 9

Can be used to explain independence if a Bernoulli trial fails the “independence” criteria

Question 10

Bernoulli Trial

Answer 10

1. Two outcomes (success/failure)
2. Known probability of success
3. Trials are independent

Question 11

z-score

Answer 11

standardized score in the Normal Model

Question 12

P(A|B)

Answer 12

Question 13

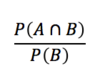
Normal Model

Answer 13

Continuous Random Variable Distribution

Also called the Normal Probability Density Function

Used to find probabilities with z-scores

Question 14

65-95-99.7 Rule

Answer 14

65% of the population is between 1 standard deviation from the mean.

95% of the population is between 2 sd’s from the mean.

99.7% of the population is between 3 sd’s from the mean.

Question 15

Percentile

Answer 15

The percent of the population LESS THAN a certain number.