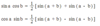Trigonometry Flashcards
Length of Line
Midpoint of Two Points
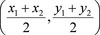
Pythagorean Theorem in terms of
sin & cos
sin2x + cos2x = 1
tan2x + 1 = sec2x
cot2x + 1 = csc2x
even and odd f(-x) = -f(x)
cos(-t) = cos t ; sec (-t) = sec t EVEN
sin (-t) = -sin t ; csc(-t) = -csc t ODD
tan (-t) = -tan t ; cot (-t) = -cot t ODD
Graph of y = sin x
Graph of y = cos x
Amplitude and Period
y = A sin (w x) & y = A cos (w x)
IAI = amplitude
&
2π/w = period
Graph of y = tan x
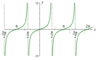
Graph of y = cot x
Graph of y = csc x
Graph of y = sec x
Domain and Range
sin(sin-1x) = x
sin-1(sin x) = x
sin(sin-1x) = x ; x –> [-1,1]
sin<sup>-1</sup>(sin x) = x ; x --\> [-π/2 , π/2]
Domain and Range
cos(cos-1x) = x
cos-1(cos x) = x
cos(cos-1x) = x ——–> x -> [-1,1]
cos-1(cos x) = x ——–> x -> [0,π]
sin-1 = y sin y = 1
Domain and Range
tan(tan-1 x) = x
tan-1(tan x) = x
tan(tan-1 x) = x ———> x -> all reals
tan-1(tan x) = x ———-> x -> [-π/2 , π/2]
A/B = C/D Then….
AD = BC
(a2-b2) ===
(a3-b3) ===
(a4-b4) ===
(a2-b2) = (a+b)(a-b)
(a3-b3) = (a-b)(a2+ab+b2)
(a4-b4) = (a-b)(a+b)(a2+b2)
Sum & Difference
cos (a+b)
cos (a-b)
cos (a+b) = (cos a)(cos b) - (sin a)(sin b)
cos (a-b) = (cos a)(cos b) + (sin a)(sin b)
Sum and Difference
sin (a+b)
sin (a-b)
sin (a+b) = (sin a)(cos b) + (sin b)(cos a)
sin (a-b) = (sin a)(cos b) - (sin b)(cos a)
Sum and Differnce
tan (x+y)
tan (x-y)
Double Angle
sin (2a) =
cos (2a) =
cos (2a) =
cos (2a) =
tan (2a) =
sin (2a) = (2sin a)(cos a)
cos (2a) = cos2a - sin2a
cos (2a) = 1 - 2sin2 a
cos (2a) = 2cos2 a - 1
tan (2a) =
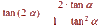
Half Angle
sin (a/2) ===
cos (a/2) ===
tan (a/2) ===
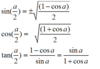
Product - to - Sum Formulas
(cos a)(cos b) =
(sin a)(sin b) =
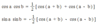
Sum - to - Product formula
sin a + sin b =
sin a - sin b =
Unit Circle BITCH
Product - to - Sum
(sin a)(cos b) =
(cos a)(sin b) =
Sum - to - Product Formula
cos a + cos b =
cos a - cos b =
tan a + tan b =
