Transformations

Question 1

What are shifting in functions, and how do they work?

Answer 1

Shifting is when a function is affected by a ADDING OR SUBTRACTING value/s.

Depending on the value’s position in the equation, it will either shift vertically or horizontally.

Question 2

What is a Vertical Reflection?

Answer 2

A vertical reflection happens when the whole function becomes negative. An example would be if the function is f(x)=x²+7 then the vertical reflection would be g(x)=-(x²+7)

Question 3

What is a horizontal Reflection?

Answer 3

A horizontal reflection (left/right) happens when just the x-part of function becomes negative.

An example if the function was f(x)= x²+7 the function when reflected would be g(x)= f(-x)=(-x)²+7.

Question 4

What is a Horizontal stretch?

Answer 4

A horizontal stretch happens when a value multiplies by the X in a function. An example of this is g(x)=f(2x) (keep in mind it can be multiplied by a fraction)

Remember that the scale factor is what the coordinates are multiplied by, but inside of the function, it’ll be upside-down.

Question 5

What is a Vertical stretch?

Answer 5

A vertical stretch (up/down) happens when a value multiplies a whole function. An example of this is g(x)= 2f(x) (keep in mind it can be multiplied by a fraction)

Question 6

How do you have to change the function “f(x)” if you want to shift it horizontally? (For example, to the right by 3 or by the left by 3.)

Answer 6

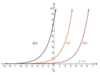
You put a “-h” in with the x term.

f(x)=2^x

g(x)=f(x+3)=2^x+3

h(x)=f(x-3)=2^x-3

Question 7

How do you have to change the function “f(x)” if you want to shift it vertically? (For example, up or down by 3.)

Answer 7

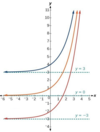
You put a “+k” at the end.

f(x)=2^x

g(x)=f(x)+3=2^x+3

h(x)=f(x)-3=2^x-3

Question 8

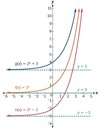
How do you have to change the function “f(x)” if you want to reflect it in the x-axis (aka “vertically”)?

Answer 8

You multiply the whole function by -1.

The new function is -f(x).

Question 9

How do you have to change the function “f(x)” if you want to reflect it in the y-axis (aka “horizontally”)?

Answer 9

You multiply the x-part by -1.

The new function is f(-x).

Question 10

How do you have to change the function “f(x)” if you want to stretch it vertically by a scale factor “a”?

Answer 10

You multiply the whole function by a.

If a is bigger than 1, it’s going to stretch the function so that it’s taller.

If a is smaller than 1, it’s going to compress the function so that it’s shorter.

Question 11

How do you have to change the function “f(x)” if you want to stretch it horizontally by a scale factor of “b”?

Answer 11

You multiply the whole x-part by 1/b. (Be careful that you first factor b out of a horizontal shift, if necessary.)

Question 12

Where is the vertex and line of symmetry for

f(x)=a(b(x-h)²)+k?

Answer 12

Vertex: (h, k)

Line of symmetry: x=h

Question 13

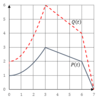
How would you describe the transformation from P(t) to R(t)?

Answer 13

This is a horizontal stretch with a scale factor of 1/2. (Notice that each point of R is half as far from the axis as P.)

So R(t)=P(2t)

Question 14

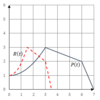
How would you describe the transformation from P(t) to Q(t)?

Answer 14

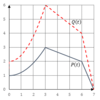
This is a vertical stretch with a scale factor of 2. (Notice that each point of Q is twice as far from the axis as P.)

So Q(t)=2P(t)

Question 15

What type of transformation does the following function represent?

f(x)=(x-2)²+2

Answer 15

It translates the x² function to the right by 2 and up by 2.