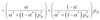Topic 2: Salter Model

Question 1

What is the numeraire in the Salter model?

Answer 1

P_T = 1

Question 2

What is the equation for the real exchange rate?

Answer 2

eR = EP/P*

Question 3

Explain the HOS Model

Answer 3

Two good model with two economies.

Countries tend to produce on their comparitive advantage.

Taxes do not effect the real exchange rate.

Both countries face the same prices.

Question 4

How is the Salter model formulated?

Answer 4

By joining together the goods X & Y into a single tradeable good T, produced by one industry. Corrispondingly there is a single nontradeable good N, produced by one industry.

It is assumed P_X:P_Y is held constant.

Question 5

Show a salter diagram, where there is a balance on the trade account. Explain the features of the model. Show the equation for the slope of the production frontier

Answer 5

Note that by definition, the consumption of N must be equal to the production of N.

As there is a balance on trade, the consumption of T is equal to the production of T (though goods X & Y may be intertraded – though at a constant price)

Question 6

Show a Salter diagram with a current account deficit. Label GDP & GNE

Answer 6

Note that GNE = A = C + I + G.

Question 8

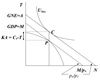
In the Salter Model, show how a decrease in the current account deficit changes the equilibrium in the model

Answer 8

Given that both goods are normal, the new consumption equilibrium will be lower in both C_N & C_T. The slope of the terms of trade line has decreased, indicating a decrease in P_N as P_T = 1. Therefore, there has been a depreciation (Must explain why for a good response).

So:

• GDP Falls (in terms of T)
• GNE Falls even more (in terms of T)

Question 9

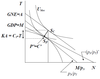
Show the effects of a resource discovery or tradeables productivity increase in the Salter model.

Answer 9

• The terms of trade line becomes steeper - so a real appreciation
• Increase in GDP in terms of T
• Increase in welfare (higher utility curve)

Question 10

Show the effects of a microeconomic reform / nontradeables productivity increase in the Salter model.

Answer 10

• Real depreciation.
• Ambigous GDP change in terms of T, as M may have increased or decreased, since P_N has decreased, but N & T has increased (M = P_TT + P_NN)
• Welfare increase
• We can think of this as a reduction it the price of local production compared with abroad, making the domestic economy more ‘competitive’

Question 11

Show mathematically why in the Saler model, a decrease in P_N represents a real depreciation.

Answer 11

PY = P_Y(p_T,p_N) = αp_T + (1-α)P_N

e_R = E P_Y/P_Y* = E (αp_T* + (1-α)P_N) / (α*p_T + (1-α*)P_N*)

As p_T = p_T*/E

e_R = (αp_T* + E(1-α)P_N) / (α*p_T + (1-α*)P_N*)

As P_T = 1, and E=1 (World without currency)

e_R = ^{α + (1-α)P_N}⁄_{α* + (1-α)PN*}

Shown in the final form below. As all the foriegn terms are exogenousm we need only consider P_N for changes