Thin Films - Review of Materials Science Flashcards
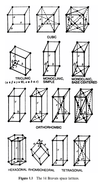
What is a Bravais space lattice?
How many types are there?
How many crystal systems does this translate to? Name them.
A geometrical concept used to define an infinite array of discrete points generated by a set of discrete translation operations described by:
R = n1a1 + n2a2 + n3a3
14 types of Bravais space lattice
7 crystal systems
What is the Miller indices?
Give the Miller indices notation for a crystal plane and family of equivalent planes.
Give the Miller indices notation for a crystal direction (normal to plane) and family of equivalent directions.
A triad of numbers that gives a family of latttice planes for a crystal system.
A crystal place is given by (hkl) and a family of equivalent planes is given by {hkl}.
Crystal direction is [hkl], normal to (hkl) plane, and family is , normal to {hkl}.
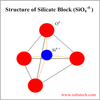
Describe the structure of amorphous SiO2.
What are the densities of quartz vs. silica glass?
A random 3D network of tetrahedra, each one featuring a central Si atom bonded to four vertex O atoms, (SiO4)4-. The O atoms are shared by two Si atoms, creating the pivotal links between neighboring tetrahedra.
Quartz = 2.65 g·cm-3
Silica glass ~ 2.2 g·cm-3
Name the four geometrical classifications of defects and give examples of each.
Point defects: vacancy, interstitial, Frenkel, substitutional, antisite, topological, dangling bond
Lines defects: screw, edge
Planar defects: grain boundaries, stacking faults
Bulk defects: voids, precipitates
Explain how vacancies form and the equation governing the expected total fraction of unoccupied sites as a function of temperature.
Is it possible to create a solid with zero vacancies?
Vacancies are a thermodynamic defect. It isn’t possible to create a solid completely free of vacancies.
How do grain boundaries (GB) affect atomic processes and reactions (e.g. diffusion, phase transformations, corrosion, precipitation, impurity segration, mechanical relaxaton)?
Why are GBs in thin films even more reactive?
GBs tend to accelerate these atomic processes because they are more energetic, like atoms at the surface of a material.
GBs tend to by a factor of 100 smaller in thin films (0.01-1 µm) as compared to bulk materials.
Why do widely separated atoms condense to form solids?
How is a solid decomposed?
Eb must be supplied
What happens to electron energy levels as atoms are brought closer together?
Why?
The energy levels split as they are brought closer to one another because of the Pauli Exclusion Principle, which states no two electroncs can exist in the same state.
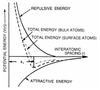
Draw the potential energy of atoms as a function of interatomic spacing and explain the key features of this graph.
What is the significance of the interatomic spacing at Eb, the bonding energy?
What is the significance of the curvature of the potential energy around Eb?
At Eb, r = a0, which represents the spacing of a solid.
The curvature around a0 is the elastic stiffness of a solid.
Name and describe the four important types of bonding in solids, including attractive/repulsive mechanisms.
First three are strong, intramolecular forces.
Metallic: Valence electrons form collective free-electron cloud or gas, attraction between free-electron gas and positive ion cores overcomes repulsive electron-electron interactions.
Ionic: Normally formed by compounds with strongly electropositive and electronegative elements (e.g. metals and nonmetals, respectively). Attraction occurs via Coulombic pair electrostatic interactions. Characterized by high Eb and melting points and poor electrical conduction (electrons are bound).
Covalent: Occurs in elements and compounds and is due to hybridization of electron wave function and the resulting bonds are very strong, resulting in materials with high melting points.
Intermolecular (weak) bonding: Primary example is van der Wals forces, or eak molecular forces due to dipole-dipole charge interactions drive attraction. Characteristic of many organic molecules like methane (CH4) and inert gas atoms. Other examples include the H bond (bond between two permanent dipoles), London dispersion force and cation-pi interaction.
Give the Gibbs free energy function (G) and explain what it tells us.
How can this be related to the 2nd Law of Thermodynamics?
What is the significance of ΔG = 0?
G = H - TS
H is enthalpy, T is absolute temperature, S is entropy.
It can be used to tell us the feasibility of a reaction from an initial state to a final state using:
ΔG = ΔH - TΔS
The 2nd Law of TD tells us that spontaneous reactions occur at constant T and P when ΔG < 0.
At ΔG = 0, the system is at equilibrium.
For a chemical reaction of three substances, given by:
aA + bB → cC
Give the free energy of individual reactance/product atomic or molecular species.
Give the free energy change of the entire reaction.
What happens when ai/ai(eq) > 1? And for ai/ai(eq) < 1?
Gi = Gi0 + RT·lnai
R is the gas constant, Gi0 is the free energy of the species i in it’s reference or standard state (e.g. 1 atm., t = 298C) and ai is an effective TD concentration that reflects the change in the species when it isn’t in its reference/standard state.
ΔG = cGc - aGa - bGb = ΔG0 + RT·ln[(aCc)/(aAa·aBb)]
What is an Ellingham diagram?
A diagram that shows the free energy of oxide formation for metals as a function of temperature.
Given the following from an Ellingham diagram, explain whether Cu or Al is the better choice for deposition onto SiO2.
What is a phase diagram and what does it tell us?
It’s a type of chart used to show conditions at which thermodynamically distinct phases (e.g. solid, liquid, gas) can occur at equilibrium for pure elements, compounds and even materials with variable (but homogeneous) composition (e.g. alloys), typically as a function of pressure, temperature and composition.
Give the equation of Fick’s first law, explain its meaning and key assumptions.
Is the diffusion coefficient constant?
Give the equation of Fick’s second law, explain its meaning and key assumptions.
Consider an initially pure thick film into which a solute diffuses from the surface. Give the initial and boundary conditions for modeling diffusion using Fick’s laws.
Give the boundary conditions for a constant and limited source.
Give the solutions for each of these cases (constant and limited source).
When does the “infinite matrix” assumption not hold up?
The “infinite matrix” assumes the film, or substrate, into which the solute diffuses is very large compared to the extent of diffusion. When (Dt)1/2 becomes large compared to the film thickness, this assumption is no longer valid.
Give the equations for the net flux from one crystallographic plane to a neighboring plane and explain.
Compare this to Fick’s Law.
(1/6) refers to the six directions, ν is vibrational lattice frequency (≈1013 s-1), Em is the vacancy jump or migration energy per atom, Ef is the energy required to remove atoms from interior sites, a0 is the lattice parameter, C is atomic concentration
exp(-Ef/kt) is the fraction of vacancy sites and v·exp(-Em/kt) is the number of times per second an atom successfully reach the activated state (vacancy site)
Draw and explain the free energy variation in a crystalline solid in the absence of an applied field and with an applied field.
Give three examples of such fields.
Three examples include stress fields, electric fields and interfacial energy gradients.
Give the following information, where rN is the net rate at which atoms pass from one location (e.g. crystallographic plane) to another), extract the Nernst-Einstein equation and explain important applications.
The term in brackets are essentially diffusivity (D), where GD can basically be equated to ED, (2ΔG/a0) is a measure of the applied force and the Nerst-Einstein equation is given by v = DF/RT (where v is atomic velocity).
Explain how the theory of atom transport in a force field can be applied to chemical rate theory.
What are the requirements for a reaction to proceed?
For a reaction to proceed to the right (as shown), CP/CR > 0 and ΔG = (GR - GP) > 0.
