Theory Flashcards
What are some recent innovations of NMR?
What do these allow us to do?
Innovations:
Cryogenic NMR probes, very low noise amplification and rf electronics and other innovations make it possible to routinely study macromolecules at micromolar concentrations and small molecules at high nanomolar concentrations. This makes new technologies much more feasible:
- Fragment based drug discovery
- Metabolomics
- small molecule NMR
- NMR of natural products at nM concentrations
- solution state NMR of protein complexes
1. High homogeneous magnetic fields. Sensitivity α B03/2
2. Cryogenic probes have improved sensitivity by about 4.5x in ethyl benzene and 3x in H2O
3. Dynamic Nuclear Polarization (DNP) in very specialized cases improves sensitivity by 200x
4. CSA/Dipole and methyl TROSY pulse sequences make it possible to interrogate protein complexes as large as the proteasome (MDa molecular weights)
What is NMR?
NMR spectrum is a plot of the intensity of absorption (or emission) on the vertical axis against frequency on the horizontal axis.
NMR spectra are unusual in that they appear at rather low frequencies, typically in the range 10 to 800 MHz, corresponding to wavelengths from 30 m down to 40 cm. This is the radiofrequency(RF) part of the electromagnetic spectrum which is used for radio and TV broadcasts, mobile phones etc.
Why is the chemical shift scale used?
It is usual in spectroscopy to quote the frequency or wavelength of the observed absorptions; in contrast, in NMR we give the positions of the lines in ‘ppm’ using the chemical shift scale.
The reason for using a shift scale is that it is found that the frequencies of NMR lines are directly proportional to the magnetic field strength. So doubling the field strength doubles the frequency. This field dependence makes it difficult to compare absorption frequencies between spectrometers which operate at different field strengths, and it is to get round this problem that the chemical shift scale is introduced.
On this scale, the positions of the peaks are independent of the field strength.
What is the role of the reference peak? How is this used to calculate chemical shift?
The chemical shift scale is set up first by agreeing a simple reference compound , a line from which is taken to define zero on the chemical shift scale. For 1H and 13C this reference compound is TMS. The choice of reference compound is arbitrary, but subject to careful international agreement so as to make sure everyone is using the same compound and hence the same origin on their shift scales.
The position of a peak in the spectrum is specified by measuring its frequency separation from the reference peak, and then dividing this difference by the frequency of the reference peak. As we are taking the ratioof two frequencies, the field dependence cancels out. The ratio thus specifies the position of a line in a way which is independent of the applied field, which is what we require.
Expressed mathematically, the chemical shift δ is given by (picture)
where υ is the frequency of the NMR line in question and υref is the frequency of the line from the agreed reference compound. Clearly, the line from the reference compound will appear at δ = 0.
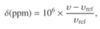
What are HTS coils? What are they used for?
Provide superior sensitivity over smaller volumes - one of the more recent innovations for NMR
“We report a 600-MHz 1-mm triple-resonance high-temperature-superconducting (HTS) probe for nuclear magnetic resonance spectroscopy. The probe has a real sample volume of about 7.5 μl, an active volume of 6.3 μl, and appears to have the highest mass sensitivity at any field strength. The probe is constructed with four sets of HTS coils that are tuned to 1H, 2H, 13C, and 15N, and there is a z-axis gradient. The coils are cooled with a conventional Bruker CryoPlatform to about 20 K, and the sample chamber can be regulated above or below room temperature over a moderate range using a Bruker variable temperature unit. The absolute S/N for 0.1% ethylbenzene is approximately 1/3 that of a conventional 5 mm probe with just 1/70 of the sample volume. We demonstrate the utility of this probe for small molecules and proteins with 2D spectra of just 1.7 μg of ibuprofenand 400 μM 15N-labeled ubiquitin.”
Journal of Magnetic Resonance 179 (2006) 290–293
Discuss the innovation of new superconducting magnets. What approximate field are these at?
Why does signal to noise ratio improve?
What happens if this is a heteronuclear experiment?
https://nationalmaglab.org/magnet-development/magnet-science-technology/magnet-projects/40-tesla-scm
Discuss the innovation of cryogenic probes: What are these and how do they improve NMR experiments?
The transmit/receive coils & tuning and matching circuits are maintained at a very low temperature (~20 K) in order to reduce the noise contributions resulting from the random thermal motion of electrons in the conductors (Johnson-Nyquist noise). The resistivity of pure metals decreases further with lower temperature, which additionally reduces noise. Preamplifier, filters and transmit-receive-switches are also cooled in order to improve the noise figure of the electronic components. Cryoprobes can improve the sensitivity by a factor of 3-6 over conventional (room temp) probes with comparable operation ranges of temperature.
What are some new opportunities that are possible with cyogenic probes?
What is dynamic nuclear polarization?
How do we convert from chemical shift to frequency?
From this it is clear that a peak at δ ppm is separated from the reference peak by 10–6 × δ × υref. It follows that two peaks at shifts δ 1 and δ 2are separated by a frequency of 10–6 × ( δ 1 – δ 2) × υref.
It is usual to express the frequency of the reference peak in MHz (= 106 Hz). When this is done the factor of 10–6 cancels and the frequency separation in Hz is simply
frequency separation (Hz) = chemical shift difference (ppm) * vref (in MHz)
So, for example, if the reference frequency is 500 MHz, then two peaks at 2.3 and 1.8 ppm are separated by (2.3 – 1.8) × 500 = 250 Hz.
Put even more simply, if the frequency of the reference peak is 500 MHz then 1 ppm corresponds to 500 Hz; if the reference peak is at 800 MHz,1 ppm corresponds to 800 Hz. The conversion from ppm to Hz is thereforerather simple.
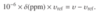
What is off-set frequnecy?
The RF circuits in virtually all NMR spectrometers are arranged in such a way that the frequencies of the peaks in the spectrum are not measured absolutely but are determined relative to the receiver reference frequency. This reference frequency can be set quite arbitrarily by the operator of the spectrometer; typically, it is placed somewhere in the middle of the peaks of interest.
It is important to realize that this receiver reference frequency has got nothing to do with the resonance from the reference compound; the receiver reference can be placed anywhere we like. The usual arrangement is that when the full spectrum is displayed, the receiver reference frequency is in the middle of the displayed region, so the frequencies of the peaks can be positive or negative, depending on which side of the reference frequency they fall.
The frequency of a peak relative to the receiver reference frequency is called the offset frequency(or, for short, the offset) of the peak. This offset frequency υoffset is given by [image]
where υ is the frequency of the peak of interest and υrx is the receiver reference frequency (‘rx’ is the traditional abbreviation for receiver). We see from this definition that the offset frequency can be positive or negative,
it is usually sufficiently accurate to divide, not by the frequency of the line from the reference compound (υref), but by the receiver reference frequency, υrx
Discuss NMR line shape, width and integrals:
The lineshape is entirely positive and is symmetrical about the maximum. The breadth of the line is specified by quoting its width at half of the peak height.
This reduction in peak height also means that the signal-to-noise ratio of the spectrum is reduced.
Image: Illustration of how the ability to resolve two lines depends on their separation relative to the linewidth. In (a) the separation υ is twice the linewidth, W ; the two peaks are clearly resolved. In (b) the separation has decreased so that it is equal to 1.5 times the linewidth and as a result the ‘dip’ between the two lines is less pronounced. Further reduction in the separation makes the dip even smaller,as in (c) where the separation is equal to the linewidth. Finally, in (d) where the separation is half of the linewidth, the two peaks are no longer distinct and a single line is seen.
What is scalar coupling?
Each doublet is split by the same amount, a quantity referred to as the coupling constant , J. It is found that the values of coupling constants are independent of the field strength; they are always quoted in Hz.
- a) The original resonance at ν1, is split due to the fact that the second nuclear spin has one of two states. b) Assuming there are two separate scalar couplings between spin-1 and 2 other spins, we can calculate the multiplet structure for three spin 1/2 coupled spins, as shown.*
- Multiplet spectra are trivial to predict in the weak coupling limit (where the coupling, J12, is far less than the difference between the frequencies of the two spins). As the coupling becomes comparable to the chemical shift difference, the shape of the multiplet becomes more complicated, though this can be easily accounted for in line shape predictions. Scalar couplings are field independent.*
Tree diagrams: Illustration of how multiplets are built up as a result of scalar coupling.
The final thing to note from Fig. 2.8 on the previous page is that since the doublet and the doublet of doublets are both from one spin, the integral of both must be the same. So, adding the second splitting to form the doublet of doublets reduces the intensity of the lines by a factor of two.
While couplings certainly provide useful information, at times they can be troublesome as the presence of many couplings will result in complex broad multiplets. This is particularly the case when observing 13C spectra of organic molecules in which any one 13C is likely to be coupled to several protons.
The effect of all of these 13C–1H couplings can be removed if, while the 13C spectrum is recorded, the protons are irradiated with a broadband decoupling sequence. Such sequences generally involve continuous irradiation of the protons with a carefully designed repeating set of pulses of particular phases and flip angles. The most commonly employed sequence is called WALTZ–16, although there are many more which can be used. Such broadband decoupling essentially sets all of the 13C–1H couplings to zero,
Show the difference between weak and strong coupling
All we have said so far about the multiplets which arise from scalar coupling is applicable only in the weak coupling limit. This limit is when the frequency separation of the two coupled spins is much larger in magnitude than the magnitude of the scalar coupling between the two spins.
For example, suppose that we record a proton spectrum at 500 MHz and that there are two protons whose resonances are separated by 2 ppm and which have a coupling of 5 Hz between them. As explained in section 2.1.2 on page 7, the frequency separation between the two lines is 2 × 500 = 1000 Hz. This is two hundred times greater than the coupling constant, so we can be sure that we are in the weak coupling limit. The coupling between different isotopes (e.g. 13C and 1H) is always in the weak coupling limit on account of the very large frequency separation between the resonance frequencies of different isotopes (usually of the order of several MHz).
On the other hand, if the frequency separation of the resonances from two coupled spins is comparable with the coupling constant between them, we have what is called strong coupling.
Unless we say otherwise, everything described in this book applies only to weakly coupled spin systems.
Disucss how a basic NMR experiment is recorded:
The way we actually record an NMR spectrum using a pulsed experiment is shown in Fig. 2.9. First, a delay is left in order to allow the spins to come to equilibrium; this is called the relaxation delay , tr. Typically this delay is of the order of a few seconds.
Next, a very short burst, typically lasting no more that 20 μs, of high power RF is applied. This excites a transient signal known as a free induction decay or FID, which is then recorded for a time called the acquisition time , tacq which usually lasts between 50 ms and a few seconds. Finally, Fourier transformation of the FID gives us the familiar spectrum.
The NMR signal tends to be rather weak, so that it is almost never the case that the spectrum from a single FID has sufficient signal-to-noise to be useful. In order to improve the signal-to-noise ratio we use time averaging. The idea here is to repeat the experiment many times and then add together the resulting FIDs. The signal part of the FID simply adds up so that after N experiments the signal will be N times stronger. However, the noise, because it is random, adds up more slowly – usually increasing as the sqrt(N) . Overall, then, repeating the experiment N times gives an improvement in the signal-to-noise ratio by a factor of sqrt(N).
We usually describe this by saying that N ‘transients’ or ‘scans’ were recorded. Calling each experiment a scan is something of a misnomer, but it is an historic usage which has stuck firmly.
Discuss motion in a circle
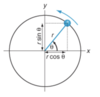
A good way to start is to think about a particle moving with constant speed along the circumference of a circle of radius r. Imagine a line joining the centre of the circle to the particle – this line is best described as a vector. As the particle moves around the circle, the position of the particle changes constantly but we can specify exactly where it is simply by giving the angle through which the vector has rotated.
At time zero the particle is on the x- axis; after some time, the particle has moved so that the vector joining it to the origin makes an angle θ to the x- axis. From the diagram, it is clear that the x- coordinate of the particle is r cos θ; and the y –coordinate is r sin θ.
Another way of looking at this is to say that the x- component of the vector is r cos θ, where by ‘component’ we mean the projection of the vector onto the axis. This projection is found by drawing a line from the tip of the vector and which is perpendicular to the x- axis; where this line cuts the x- axis gives the component along that axis.
Imagine a particle following a circular path about the origin; here the rotation is anti–clockwise. At time zero, the particle starts on the x- axis and after a certain time it has rotated through an angle θ, measured from the x- axis. If the circle is of radius r , the x- and y- coordinates are r cos θand r sin θ,respectively. These coordinates are also the x- and y- components of the vector from the origin to the particle.
Discuss this graph:
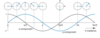
Figure 2.15 shows these x- and y- components plotted against the angle θ; above the graph is shown the corresponding position of the particle. Rather than specifying the angle in degrees we have chosen to give it in radians. Recall that there are 2 πradians in a complete revolution i.e. 360°. So, θ = π/2 corresponds to one quarter of a revolution or 90°. Similarly, θ = 3π/2 corresponds to three quarters of a revolution, or 270°.
The rotation of the particle, which is simply a steady increase in the angle θ, gives rise to x- and y- components which are oscillating as cosine and sine functions. We see that there is thus a strong connection between rotational and oscillatory motion.
Fig. 2.15 Illustration of how the x- and y- components of the vector specifying the position of a particle moving round a circular path vary with the angle θ, as defined in Fig. 2.14. The x- and y- components vary as cos θ and sin θ, and are shown by grey and blue lines, respectively. For some selected angles, the position of the particle is shown above the graph; the horizontal axis gives the angle θ in radians, expressed as multiple of π. Note that the x- and y- components can be positive and negative, and that after a complete revolution, θ = 2π, the pattern repeats.
What is frequency of motion for NMR?
We started out by supposing that the particle was moving around the circle at a constant speed. Suppose that it takes a time tto complete one revolution – this is called the period. This period is the same for the sine and cosine waves which describe the position of the particle and it is the time after which they repeat.
The frequency of the rotation or oscillation, υ is simply v=1/T
So a fast oscillation or rotation, which has a short period, corresponds to a high frequency. Another way of thinking about the frequency is to see it as the number of cycles or oscillations per unit time.
The period is specified in seconds (s), so the frequency has units s–1 or, equivalently, Hertz (symbol Hz). Thus an oscillation or rotation with a period of 0.0013 s corresponds to a frequency of 769 Hz. In words, this means that in 1 s (that is, a unit of time) the oscillation goes through 769 complete cycles.
What is the difference between angular frequency and frequency?
What is the phase?
There is another way of expressing the frequency, which is to give it in radians per second; this is called the angular frequency , ω. Suppose that the period is T. During this time the angle θ increases by 2 πradians so the angular frequency is
w= 2*pi/T
f the time is in seconds, ω will be in radians per second i.e. rad s–1.
Fig. 2.16 The position of the particle is described by the angle ϕ which is called the phase. Here, the phase, measured from the x- axis, is 225° or 1.25 π radians. Thought of in terms of the oscillating x- and y- components, the phase tells us how far along the wave we have travelled; on the graph, the vertical dashed line shows the phase, ϕ, corresponding to the diagram above. As before, the grey and blue lines represent the x- and y- components, respectively.
The usual convention is to use the symbols f , F or υ (Greek ‘nu’) to represent frequencies in Hz, whilst ω and Ω (Greek lower and upper case ‘omega’) are used to represent frequencies in rad s–1.
Discuss how the x and y signal change is the magentisation vector begins at different values of the phase:
Suppose that our particle depicted in Fig. 2.14 on the facing page starts on the x- axis and then rotates through an angle ϕ, as shown in Fig. 2.16. We describe this situation by saying that the particle has ‘acquired a phase ϕ’. In this context, phase is just a way of saying how far the particle has proceeded around the circle. If we think about the sine and cosine functions which represent the x- and y- components, the phase just tells us how far along the oscillation we have proceeded.
Fig. 2.17 Illustration of how a phase angle can be used to describe the starting position of our particle. The top row shows the starting positions at time zero; in (a) the phase, ϕ, is π/4 radians or 45°, in (b) the phase is π/2 radians or 90°, and in (c) the phase is p radians or 180°. The bottom row shows the time dependence of the x- and y- components (grey and blue lines, respectively) as the particle moves from its starting position. Note that in all cases theses components are just those shown in Fig. 2.15 on page 16 shifted to the left by differing amounts.
If the particle is moving at a constant angular frequency of π rad s–1 , then after time tthe angle (in radians) through which the particle has moved is just
EXAM STYLE QUESTION:
Two 23Na NMR resonances are observed to be 0.5 ppm apart on a 600 MHz (1H NMR) NMR spectrometer.
a) Calculate the separation in Hz and rads/s. Use NMR Periodic table
b) Assuming S/N is proportional to I(I+1)y5/2B03/2 calculate the relative S/N of a sodium NMR experiment to that of a 1H NMR experiment (assuming identical delay times). How many times more scans would thus be required to obtain equivalent S/N?
EXAM STYLE QUESTION:
- Two spins differ in frequency by 75 Hz. Calculate how long it takes for them to dephase by π radians.
EXAM STYLE QUESTION:
- Two equivalent methylene protons are separated coupled to spin B (JAB=10 Hz) and spin C (JAC=20 Hz). Assuming weak coupling work out the multiplet using a tree diagram. Repeat the above exercise assuming spin B and spin C are deuterons (I=1).
How can we represent phases using complex numbers?
EXAM QUESTION:
In a 1H NMR spectrum the peak from TMS is found to occur at 500.134 271 MHz. Two other peaks in the spectrum are found at 500.135 021 and 500.137 921 MHz; compute the chemical shifts of these two peaks in ppm.
Given that the receiver reference frequency is 500.135 271 MHz, recompute the chemical shifts of the two peaks using Eq. 2.3 on page 8; comment on your answers.
What would the frequency separation, in Hz and in rad s-1, be between these two peaks if the spectrum were recorded using a different spectrometer which operates at 400 MHz for protons? The receiver reference frequency for this spectrometer is 400.130 000 MHz.
Exam style question:
Following the style of Fig. 2.17 on page 18, make sketch graphs of the x- and y- components of a rotating particle as a function of time for the case where the starting phase φ is: (a) 0°; (b) 135°; (c) 2 πradians; (d) 3π/2 radians. In each case, comment on the form of your graphs, noting particularly whether they are simple sine or cosine functions.
Exam style question:
In Fig. 2.17 (c) on page 18 the y- component is r sin (ωt+ π). Using the same approach as on page 19, show that this y- component can be written more simply as – r sin (ωt).
What is the hamiltonian used to describe the interaction of nuclear spin and the magnetic field?
How does this change for the two spin states?
Each energy level has associated with it a different wavefunction and, just as it is commonly implied that the molecule must be in one of the energy levels, it is also often implied that the wavefunction of the molecule must be the one associated with that level.
The energy levels and associated wavefunctions for a particle constrained so that it can only move between x = 0 and x = L – the so-called ‘particle in a box’. We are tempted to slot the particle into one of the energy levels and hence give it the associated wavefunction. However, this is not what quantum mechanics specifies; rather the wavefunction which describes the particle is in general a mixture of the wavefunctions corresponding to each energy level.
In fact, the wavefunction for the molecule is generally a mixture of the wavefunctions associated with the energy levels: such a wavefunction is often called a mixed state or a superposition state.
For a nuclear spin in a magnetic field of strength B0applied along the z-axis, the Hamiltonian which represents the energy of interaction between the spin and the magnetic field is
where γ is the gyromagnetic ratio, which is a fundamental property of the nucleus in question.
Îz is an operator which represents the z-component of the nuclear spin angular momentum. Angular momentum is a concept from classical physics where it is associated with rotational motion. For example, a mass following a circular path has angular momentum, which turns out to be a vector quantity having both a magnitude and a direction
How does the eigenvalue of the hamiltonian correspond to energy?
How do we use this to find Larmor frequency?
As we saw in section 2.6 on page 20, to convert energies from Joules to Hz, all we need to do is divide by Planck’s constant, h, and to convert from Joules to rad s−1 we divide by hbar.
How can we describe energy levels in frequency units?
How can the energy levels be desribed of a two spin system?
How can this be written as eigenvalues?
Show how energy levels of a two spin system for an energy level diragram and how these convert to spectra:
. As expected, the spectrum consists of two doublets, each split by J12 and centred at the Larmor frequencies of spins one and two.
As a result of the selection rule, each allowed transition corresponds to one of the spins ‘flipping’ from one spin state to the other, while the state of the other spin remains fixed. For example, transition 1–2 involves a spin two going from α to β whilst spin one remains in the α state. In this transition we say that spin two is active and spin one is passive and in the α spin state. As spin two flips in this transition, it is not surprising that the transition forms one part of the doublet for spin two.
On the left, the energy levels of a two-spin system; the arrows show the allowed transitions: grey arrows indicate transitions in which spin one flips and blue arrows indicate those in which spin two flips. On the right, the corresponding spectrum; each line is marked according to the two energy levels involved, which spin flips (the active spin) and the spin state of the passive spin. It is assumed that the Larmor frequency of spin two is greater in magnitude than that of spin one, and that the coupling J12 is positive.
Transition 3–4 is similar to 1–2 except that the passive spin (spin one) is in the β state; this transition forms the second line of the doublet for spin two. This discussion illustrates a very important point, which is that the lines of a multiplet can be associated with different spin states of the coupled (passive) spins. We will use this kind of interpretation very often, especially when considering two-dimensional spectra.
The two transitions in which spin one flips are 1–3 and 2–4, and these are associated with spin two being in the αand β spin states, respectively. Which spin flips and the spin states of the passive spins are shown in Fig. 3.8 for each transition.
If the coupling J12 is negative, working through the calculation gives the same four lines at identical positions as for a positive coupling of the same magnitude. This result is in accord with the observation we made earlier in section 2.3 on page 10 concerning the effect (or lack of it) of changing the sign of the coupling.
However, what does change when the coupling becomes negative are the labels of the lines, as is illustrated in Fig. 3.9. For example, transition 1–2 is now the right-hand line of the doublet, rather than the left line. From the point of view of the spectrum, what swaps over is the spin state of the passive spin associated with each line of the multiplet.
What do hamiltonians look like for the energy levels of 3 spin systems?
How does it end up like this?
There are two more transitions in our two-spin system which are not allowed by the usual selection rule and so do not appear in the spectrum; the transitions are illustrated in Fig. 3.10 on the next page. We will discover later on that, using two-dimensional NMR, we can detect these transitions indirectly.Energy levels for a three-spin system showing by the arrows the four allowed transitions which result in the doublet of doublets at the shift of spin one. The schematic multiplet is shown on the right, where it has been assumed that υ0,1 = -100 Hz, J12 = 10 Hz and J13 = 2 Hz. The multiplet is labelled with the spin states of the passive spins.
What is magetic resonance?
What gives rise to “precession” of magnetization in the presence of a magnetic field?
Why is there a net magnetization in a magnetic field associated with nuclear spins?
What causes spins to align in a magnetic field? Why aren’t they all aligned?
Can a single spin I=1/2 have any orientation in the field (i.e. not just parallel or antiparallel)? An Energy Level Description
Show curie’s law derivation for spin 1/2
Show the diference of a single spin compared to multiple spins in a diagram:
What does this tell us?
- Calculate the bulk magnetization for a spin 1⁄2 1H nuclei in a sample of water assuming a magnetic field of 14.1 Tesla and a volume of 300 μl and a temperature T=293K
An unpaired electron spin has a magnetic moment that is 750x that of a nuclear spin. How much bigger (per spin) would you expect the magnetization to be?
How we detect NMR signal
How do rf pulses cause magnetisation?
How can the rotating frame help us understand time dependance of NMR?
How does an oscillating magnetic field combine with rotating frame?
How can we calculate the effect of an off resonance pulse in the presence of an oscillating magnetic field, B1
Discuss
Thus “hard” on resonant pulses result in precession of the Magnetization along well described trajectories of duration, τ, such that ωτ=π/2, as in (a) and (b).
Offsets result in more complicated trajectories as shown in b, c, and d, as a function of increasing offsets, Δω.
Left:
The corresponding profile of Mx and My as a function of offset for a given 90 degree pulse of phase, x.
Summarize net polarisation:
What are Rf pulse callibrations?
For single hard pulses, we typically apply a given power setting and record the signal as a function of pulse length (flip angle). Clearly a 90° pulse should generate maximum signal while
In situations where we perform 1H NMR, users often calibrate their pulses from the 1H2O signal. Due to a phenomenon known as radiation damping, the trajectory of magnetization on water is not symmetrical. To calibrate pulses we often look for a null associated with the 360° pulse and then take 1⁄4 this time to estimate the 90° pulse length. It is also a good test of amplifier stability to record spectra for times that are as much as 10x the 90° pulse. A nice smooth constant sinusoid implies good RF pulse homogeneity.
How can spin echo give us information about line widths and T2 relaxation?
