Theorems

Question 1

Intermediate Value Theorem

Answer 1

Conditions: f is continuous on [a, b]

Conclusion: For every N between f(a) and f(b), there exists a number c with f(c) = N

Question 2

Extreme Value Theorem

Answer 2

Conditions: f is continuous on a closed interval [a, b]

Conclusion: f has an absolute maximum value f(c) and an absolute minimum value f(d) at some numbers c and d in [a, b]

Question 3

Rolle’s Theorem

Answer 3

Conditions:
• f is continuous on the closed interval [a, b]
• f is differentiable on the open interval (a, b)
• f(a) = f(b)

Conclusion: Then there exists a number c in (a, b) such that f ‘(c) = 0.

Question 4

Mean Value Theorem

Answer 4

Conditions:
• f is continuous on the closed interval [a, b]
• f is differentiable on the open interval (a, b)

Conclusion: There exists a number c in (a, b) with a tangent line parallel to the line between a-b.

Question 5

Continuity

Answer 5

Conditions:
• f(a) is defined
• lim {x→a} f(x) exists (both sides equal)
• lim {x→a} and f(a) are equal

Conclusion: f is continuous at a.

Question 6

Limit Definition of Derivative

Answer 6

Question 7

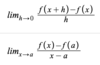
Squeeze Theorem

Answer 7

Conditions:
• f(x) ≤ g(x) ≤ h(x)
• lim {x→a} f(x) = lim {x→a} h(x) = L

Conclusion: lim {x→a} g(x) = L