The Time Value of Money (Week 2) Flashcards
Is $100 now worth the same as $100 in the future?
No, the difference is the time value of money
How do you compare projects that generate cash flows at different points in time?
You move them to the same point in time and compare their present value (value today) or compare their future value (at the same time in the future).
What is compounding?
Moving cash flows forward in time
You have a choice between:
a) Receiving $1,000 today
b) $1,250 in two years
Your bank account earns 10% p.a.
To compare (a) and (b) you think about how much money you would have in two years if you got $1000 today and invested for 2 years at 10%
1000 x 1.1 = 1100
1100 x 1.1 = 1210
As $1,250 > $1,210, option (b) would be better
What is the Future Value after n years?
What is compound interest?
The effect of “earning interest on interest”
What is equity premium?
- The equity-risk premium predicts how much a stock will outperform risk-free investments over the long term.
- Calculating the risk premium can be done by taking the estimated expected returns on stocks and subtracting them from the estimated expected return on risk-free bonds.
- Estimating future stock returns is difficult, but can be done through an earnings-based or dividend-based approach.
- Calculating the risk premium requires some assumptions which run from safe to dubious.
Suppose you have a choice between receiving $5,000 today or $10,000 in five years.
You believe you can earn 10% on the $5,000 today, but want to know what the $5,000 will be worth in five years.
Which do you choose?
In five years, the $5,000 will grow to:
$5,000 x (1.10)5 = $8,053
The future value of $5,000 at 10% for five years is $8,053.
You would be better off forgoing the gift of $5,000 today and taking the $10,000 in five years.
What is Discounting?
- Process by which we move a cash-flow back in time
- Finding the equivalent value today (the present value) of a future cash-flow
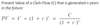
How do you calculate the Present Value of a Cash-Flow? (Equation)
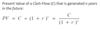
Suppose you are offered an investment that pays $10,000 in five years
The discount rate is 10% p.a.
What is the value of the investment today?
You are given a financial instrument as a gift.
It pays $1000 today and $1000 at the end of each of the next two years.
You earn a fixed 10% interest rate on your savings account (you have no other investment opportunities).
How much money would you have at the end of Y2 (start of Y3)?
$3,641
The financial instrument pays you $1000 this year and $1000 each year for the next two years.
If you can borrow and lend at a rate of 10% p.a., what would be the maximum you would be willing to pay for this financial instrument?
The maximum you would be willing to pay is $2,735.54
If you already have the future value (3641) you can calculate present value by dividing by 1.13.
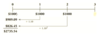
- You are thinking of entering the toothpick business
- A toothpick machine is offered to you for $5,000
- With it, you can sell toothpicks worth $4,000 in the 1st year, $3,000 in the 2nd year and $2,000 in the 3rd year.
- However, the machine costs $1,000 per year to operate
- The discounte rate is 7%
- Do you buy the machine?
What is a perpetuity?
When a constant cash flow will occur at regular intervals forever it is called a perpetuity. The value of a perpetuity is simply the cash flow divided by the interest rate.
How do you calculate Present Value of a Perpetuity?
The cash flow divided by the interest rate.
Equation for Present Value of a Growing Perpetuity equation
Determine the value of the following financial security.
Annual constant payments of $1mn
30 annual payments, starting next year.
Discount rate is 8%.
PV(annuity of C for N periods with discount rate r) = [equation]
Present value of a growing annuity [equation]
