The Nature of Stars

Question 1

What is a parsec?

Answer 1

Parsecs (pc) and lightyears (ly) are used as convenient astronomical distance units because they are very large.

• A lightyear is simple: the distance light travels in 1 year.
• A parsec is DEFINED to be that distance at which a star will have a parallax angle of 1 arcsecond – see next slide.

One Parsec (pc)

One pc is the distance from which Earth would appear to be one arcsecond from the Sun.

Question 2

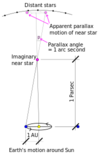
How do you determine the distance to a star?

Answer 2

If we are to know exactly how luminous is a star, then we need to know how far it is away.

• This is tricky for most stars because of variable interstellar absorption effects.
• But for nearby stars we can use Parallax.

d=1/p

where d = distance in parsecs and p = parallax angle in arcseconds NB 1 AU = 1 astronomical unit (the average Earth-Sun distance)

Question 3

Gaia - NT

Answer 3

Launched 2013

An ESA mission to measure the distance to 1000 million stars using parallax (1% of the Milky Way)

Because it is in space and not limited by the Earth’s atmospheric distortion, it can measure much smaller parallaxes.

Question 4

How do you determine the luminosity of a star?

Answer 4

Since starlight spreads out uniformly over a sphere, and we (on the earth) intercept just a part of this light, we need to multiply up to account for the whole sphere of light.

If L is the star’s absolute luminosity, and d is its distance, then, b, the apparent luminosity is given by:

b = L / (4π d²) (where 4πd² = the surface area of a sphere)

Question 5

What is the proper motion of a star?

Answer 5

• We cannot directly measure the component of velocity along the line of sight (vr) since this does not cause the position of the star on the sky to change.
• But we can determine the tangential component (vt) by observing the changing location of the star at distance d pc.
• Proper motion, μ = vt/(4.74d) arcsec/year

Question 6

Quantifying brightness - understanding the logarithmic scale

Answer 6

Magnitudes

A logarithmic based scale for quantifying brightness.

A difference of 1 magnitude corresponds to a factor of 2.5 in brightness.

A difference of 5 magnitudes corresponds to
2.5 x 2.5 x 2.5 x 2.5 x 2.5 = (2.5)⁵ ~ 100 in brightness.

• If we have two stars of apparent magnitude of m₁ and m₂, then they are related to their apparent brightness b₁ and b₂ by:

m₂ – m₁=2.5 log (b₁/b₂) …..Eqn 1

Question 7

Quantifying brightness - absolute magnitude

Answer 7

We observe apparent magnitude, m.

What we need to know is the absolute magnitude, M, of an object

The absolute magnitude is defined as the magnitude that object would have at a distance of 10pc.

So if it’s actually at a distance, d parsecs, away:

m – M = 2.5 log (b₁/b₂) from Equn 1 where b₁ is the brightness at 10 pc and b₂ is the brightness at d pc.

• • •

But also we have that b₁/b₂ = (d/10)² (brightness falls off as 1/d2) So we have (m-M) = 2.5 log (d2/100)

=2.5(log d2 – log100)

Finally we have (m–M)=5logd–5

where (m-M) is called the distance modulus to an object.

Question 8

Spread of stars of a given luminosity

Answer 8

The stellar luminosity function reveals how many stars there are of a given luminosity within a volume of 1000 cubic parsecs.

Note that the brightest star has the smallest apparent magnitude.

i.e. the magnitude scale runs backwards.

Question 9

Temperature and colour relationship

Answer 9

Stellar colours depend strongly on the temperature of the star.

Red stars are cool, blue stars are hot.

Question 10

Astronomical Filters

Answer 10

The brightness of stars is normally measured through certain standard coloured filters.

• This process is called photometry.
• The filters cover the entire visible and IR range and given letters. The most common system, the Johnson-Morgan system, uses:

UBVRIJHK

Question 11

Colour being described as magnitude differences

Answer 11

Because the magnitude scale is a logarithmic one, if we convert the brightness ratios into magnitudes then we end up with the colour being described as magnitude differences :

e.g. brightness ratio b_B/b_V is equivalent to (apparent mag B) – (apparent mag V) or just (B-V).

Question 12

Classifying stars

Answer 12

Using the spectra of stars it is possible to classify a star as a particular spectral type.

• This is done by examining the emission or absorption lines present in a stars spectrum.
• For historical reasons the sequence now used is:

OBAFGKM
This takes us from very hot to very cool stars.

Question 13

Subclassification

Answer 13

With the advent of superior spectrographs in the last 50 years it became apparent that the OBAFGKM classification needed refining.

So each class is now given a number between 0 and 9 to sub-divide the type

So we have, for example, A7, G3, B5 etc (the Sun is G2).

The key to classification is the relative strength of many different absorption lines from many different elements in the star.

Question 14

What is a Hertzsprung-Russell diagram?

Answer 14

• Discovered independently by a Danish and US astronomer in 1911
• It allows us to understand stars relative to other stars
• It allows us to see evolutionary paths for stars

The HR Diagram

Plot of stellar temperature versus luminosity – note the direction of the temperature axis.

The general locations of the more common stars are shown.

Note that our Sun sits on the Main Sequence (MS) where many stars spend most of their lives.

Question 15

Classifying a star by name

Answer 15

As can be seen from the HR diagram, temperature alone is not enough to classify a star. For example, at T=5800K a star could fall in 4 different luminosities on the diagram:

• Supergiant
• Giant
• Main-sequence
• Dwarf

Question 16

Classifying a star by luminosity

Answer 16

Stars are then further classified into different luminosity classes based upon the width of their emission lines and given a Roman numeral between I and V.

Question 17

Star classification summary

Answer 17

So we now have the full modern designation for a star. Each type name consists of three parts:

First a letter from OBAFGKM

Second a number between 0-9 as a subdivision

Thirdly a Roman number I- V indicating the luminosity class.

I-supergiant

III-giant

V-MS

For example, our Sun is a G2V type star.

Question 18

Mass - Luminosity relationship

Answer 18

For MS stars there is a strong correlation between stellar mass and luminosity:

L= constant M^3.5

For example, a star that is 10 times the mass of our Sun is many thousand times more luminous

On the HR diagram the physical parameters of MS stars change along its length.

From the bottom to the top the mass, luminosity and temperature all increase.

So temperature on the HR diagram x- axis can also be represented by the colour (B-V) of a star.