The Fundamental Theorem of Calculus, Part II (9.4.4)

Question 1

• Let f be defined on the interval [a, b]. The definite integral of f from a to b is if exists.

Answer 1

• Let f be defined on the interval [a, b]. The definite integral of f from a to b is if exists.

Question 2

• The fundamental theorem of calculus links the velocity and area problems. It enables you to evaluate definite integrals, thereby finding the area between a curve and the x-axis.

Answer 2

• The fundamental theorem of calculus links the velocity and area problems. It enables you to evaluate definite integrals, thereby finding the area between a curve and the x-axis.

Question 3

• The fundamental theorem of calculus states that if f is continuous on [a, b] and F is an antiderivative of f on that interval, then .

Answer 3

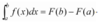
• The fundamental theorem of calculus states that if f is continuous on [a, b] and F is an antiderivative of f on that interval, then .