Tests

Question 1

How do you Conducts a Group(ing) of Signs Test?

Answer 1

1. Count number of positive deviations (n₁) of estimated values compared with observed values - i.e. (Oi - Ei)
2. Count number of negative deviations (n₂)
3. Count number of groups of runs of positive deviations **(t) **
4. Look in standard table - for n1 and n2 gives maximum number of runs n_critical for which
   p(t) < 0.05 (i.e. 5% significance),
   if t <= n_critical, reject H0,
   if t > n_critical, accept H0

More runs = better fit to data!

Question 2

How do you Conduct a Individual Standardised Deviations Test on Graduations for Data?

Answer 2

The Individual Standardised Deviations test looks for individual large deviations at particular ages.

If the graduated rates were the true rates underlying the observed rates we would expect the individual deviations to be distributed Normal (0,1) and therefore:

• EITHER only 1 in 20 z_x should lie above 1.96 in absolute value
• OR none should lie above 3 in absolute value

Question 3

Least Significant Difference (Fisher’s LSD Test)

Answer 3

Fisher’s LSD is a method for comparing treatment group means after The ANOVA null hypothesis of equal means has been rejected using the ANOVA F-test.

Pairwise comparison of the means
The LSD test involves pair wise testing of means, i.e. in turn testing hypotheses of the sort H₀ : µ_A = µ_B, H₀ : µ_A = µ_C, etc. The LSD method for testing the hypothesis H₀ : µ_A = µ_B proceeds as follows:

Comparing µ_A and µ_B

Group A contains n_A members,
Group B contains n_B members

MSW = Mean of Squares within (Mean Residual Sum of Squares) = RSS / d.f.(within) - as calculated for ANOVA

LSD_AB = t_0.05/2,DFW x √MSW(¹/_nA + ¹/_nB)

(two-sided t-test at 5% significance, with DFW degrees of freedom, where DFW is the degrees of freedom for within squares - i.e. total number of outcomes - total number of groups)

If | µ_A - µ_B | > LSD_AB
reject H₀, i.e. reject µ_A = µ_B

Question 4

What is a Z Test

Answer 4

A Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution.

Question 5

How do you Do a One Way Analysis of Variance (ANOVA)?

Answer 5

In order to compare the means of different groups of observations of random variables with a common variance, create ANOVA table and then:

Calculate F ratio score and compare with null hypothesis F score for significance level α given by:
F0 = F_{k-1, n-k, α}
F is calculated as follows:

Question 6

What is a t-test?

Answer 6

A t-test is any statistical hypothesis test in which the test statistic follows a Student’s t distribution if the null hypothesis is supported.

It can be used to determine if two sets of data are significantly different from each other, and is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known.

This is usually where a sample is too small to assume an approximation to the normal distribution.

Question 7

What is a chi-squared goodness-of-fit test, when should it be used?

Answer 7

The goodness of fit chi-square tests are used to test whether a set of data (a sample) fits a stated probability distribution.

The null hypothesis H₀ is that the data fits the distribution, H₁ that it does not. H₀ is rejected if the chi-square score exceeds the critical value from the table for degrees of freedom ν, given by:

ν = c - 1 - k

where c is the number of categories for data, k is the number of population parameters estimated to calculate frequency.

If graduating the data using standardised tables, drop a couple of degrees of freedom overall and then state this has been done.

The chi-square statistic is the sum of squares of difference between observed and expected values, divided by the expected value:

Question 8

When are you Not Allowed to do a Chi-Square Test?

Answer 8

• When more than 20% of the expected counts are less than 5 or
• when any expected count is less than 1.

In other words, you can only do a chi-square test when:

No more than 20% of the expected counts are less than 5 and all individual expected counts are 1 or greater” (Yates, Moore & McCabe, 1999, p. 734).

Question 9

How do You Test Whether the Variance of two Samples is Equal?

Answer 9

If two samples, A and B, have n_A and n_B observations, with Sample Variances S_A² and S_B^2, then it is possible to test the null hypothesis H0 (variances equal) with a two-sided F-Test:

Question 10

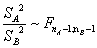
What is the Cumulative Deviations Test

Answer 10

The Cumulative deviations test is a test for bias in data graduations

Question 12

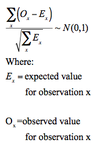
What is the t-test for comparing the means of two samples of unequal size from distributions with equal variance?

Answer 12

t-test for samples of unequal size
from distributions with equal variance

Question 13

What is the t-test for comparing the means of two samples from distributions whose variances cannot be assumed to be equal?

Answer 13

AKA Welch’s t-test

Question 14

What is a Signs Test?

Answer 14

A signs test is used to determine whether a data graduation is biased - i.e. systematically higher or lower than the data it is graduating.

In order to do the test:

1. Comparing (Oi - Ei) - observed value less expected value - if this difference is not zero, record the sign (positive / negative)
2. Count the number of non-identical pairs (m) and the number of positive signs (p)
3. Test p against a Binomial(m, 0.5) distribution (from tables in back of formula book)
   * for large samples > 25, can use normal approximation to binomial*