Test 2 - Counting & Probability Flashcards
(23 cards)
N = [Alfred, Bob, Carol, Daniel, Emma], abbreviated as N = [A, B, C, D, E] Assuming all members of the club are eligible, but that no one can hold more than one office, list and count the different ways the club could elect both a president and a treasurer. What would a list of all the possible pairs of presidents and treasurers look like? How many ways can a president and treasurer be elected?
AB, AC, AD, AE, BA, BC, BD, BE, CA, CB, CD, CE, DA, DB, DC, DE, EA, EB, EC, ED
Refer to the table below. Of the 36 possible outcomes, determine the number for which the sum (for both dice) is odd?

There are 18 outcomes where the sum is odd.
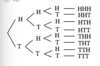
Construct a tree diagram showing all possible results when three fair coins are tossed. Then list the ways of getting the following result.
More than 2 tails.
An unusual die has the numbers 2, 2, 3, 3, 8, and 8 on its six faces. Two of these dice are rolled, and the two numbers on the top faces are added. How many different sums are possible?
The number of possible different sums is 6.
Evaluate the expression without a calculator.

(6x5)/2 = 15
Find the number of distinguishable arrangements of the letters of the word.
CENTILLION
10!/(2x2x2) = 453600
A panel containing five on-off switches in a row is to be set. Assuming no restrictions on individual switches, use the fundamental counting principle to find the total number of possible panel settings.
2x2x2x2x2 = 32
When two fair dice are rolled, there are 36 possible outcomes. How many possible outcomes would be there if three fair dice were rolled?
6x6x6 = 216
In how many ways could members of the following club line up all 10 members for a photograph? N = [James, Sandy, Jane, Ashley, Emma, Anthony, David, Evelyn, Linda, Craig]
10! = 3628800
How many ways can a male and female be selected to decorate for a party from a club consisting of nine members where three are men and six are women?
3x6 = 18
A multiple-choice test consists of 8 questions with each question having 4 possible answers. How many different ways are there to mark the answers?
4x4x4x4x4x4x4x4 = 65536
Don has six pairs of shoes, eight pairs of pants, and six shirts. If all items are compatible, how many different outfits can he wear?
6x8x6 = 288
How many ways can a president, vice-president, secretary, and treasurer be chosen from a committee or 9 people?
9P4 = 3024
How many ways can a teacher give three different prizes to three of her 28 students?
28P3 = 19656
In a race in which six automobiles are entered and there are no ties, in how many ways can the first three finishers come in?
6P3 = 120
An electronics store receives a shipment of 20 graphing calculators, uncluding 5 that are defective. Four of the calculators are selected to be sent to a local high school. How many of these selections will contain no defective calculators?
15C4 = 1365
To win at LOTTO in one state, one must correctly select 5 numbers from a collection of 48 numbers (1 through 48). The order in which the selection is made does not matter. How many different selections are possible?
48C5 = 1712304
Subject identification numbers in a certain scientific research project consist of two digits followed by two letters and then three more digits. Assume repetitions are not allowed within any of the three groups, but digits in the first group of two may occur also in the last group of three. How many distinct identification numbers are possible?
10x9x26x25x10x9x8=42,120,000
Television and radio stations use four call letters starting with W or K, such as WXYZ or KRLD. Assuming no repetitions in the second to fourth letters, how many four-letter sets are possible using either W or K and only the letters N to Z?
2x13x12x11=3,432


In how many ways could 19 people be divided into five groups containing, respectively, 1, 2, 5, 7, and 4 people?
19x153x4368x330x1 = 4190266080






