Tentamen Flashcards
What is the LS estimator of beta?
β hat = (X’X)-1X’y
What is the LS estimator of σ2?
s2 = e’e/(n-k)
How to show that beta hat (LS) is unbiased?
E(β hat) = E[(X’X)-1X’y] = (X’X)-1X’ E[y] = (X’X)-1X’X β = β
How to show that s2 is unbiased, or how to derive it?
Let B, a positive semidefinite matrix. Then we can rewrite s2 = y’By = (Xβ + u)’B(Xβ +u) = u’Bu + 2 β’X’Bu + β’ X’ BX β.
If we take the expectation of this:
E(s2) = E(u’Bu) + β’ X’ BX’ β = σ2 tr(B) + β’ X’ BX β.
Since we know that BX = 0 is satisfied if B = M (residual maker), and tr(M) = n - k, s2 = y’My/(n-k) = e’e/(n-k) is unbiased.
How to derive the variance of beta hat?
Var(β hat) = Var[(X’X)-1X’y] = (X’X)-1X’ Var(y) ((X’X)-1X)’ = (X’X)-1X’ σ2 In X’(X’X)-1 = σ2 (X’X)-1
Show that no other linear unbiased estimator of β has a lower variance.
When to use the F-statistic for testing, and what is it?
The F-statistic should be used when testing multiple linear restrictions, where R is a matrix with the formula of the restriction, and r is the value.
What is the statistic for testing a single restriction?
w is a vector of the restriction, r is the value.
What is the statistic for testing if beta equals zero?
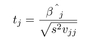
How to derive a ML-estimator?
- First create the Likelihood function (the product of n draws of the CDF)
- Take the ln of this function
- Derive it
- Equate to zero
- Possibly take the second derivative to show that it is in fact a minimum
Show the Cramer-Rao inequality, what does this mean?
It means that if an unbiased estimator achieves the lower bound it’s efficient.
What is the adjusted R2, and what is R2 (formulas)?
Note: SST = y’Ay
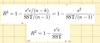
What is the difference between a model and a data generating process?
A model tries to approximate the DGP, but is does not equal the DGP (generally).
How can be shown that the normal distribution is a second order approximation around te mode?
How is σ hat, and β hat derived (using the ML)?
What is the formula for the covariance and the variance?
Cov(a, b) = E[(a - E(a))(b - E(b))’]
Var(a) = E[(a - E(a))(a - E(a))’]
What is the formula of the SST? And A?
SST = y’Ay
A = In - ɩɩ’/n
How to get the restricted ML values?
On what is the Wald, the Lagrangian Multiplier and the Likelyhood ratio test based?
Wald: Based on the idea that Rβ hat should be close to r if the null hypothesis is true.
LM: Based on the fact that the gradient q(β hat) vanishes if the null hypothesis is true, thus q(β hat) should be close to zero (for the null hypothesis).
LR: Based on the ratio of the maximized likelihood with the restriction to the maximized likelihood without the restiction, which should be close to one if the null hypothesis is true.
What is the Wald, LR, and LM test (when σ is given)?
(Rβ hat - r)’(R(X’X)-1R’)-1(Rβ hat - r)/σ2, it is chi-squared (m) distributed, where m is the number of restrictions.
How to show the order of the Wald, LM and LR tests?
What is the matrix M and what does it do?
M is the residual maker matrix, s.t. e = y - Xβ hat = My = Mu,
var(e) = var(Mu) = σ2M.
M = In - X(X’X)-1X’
How to do confidence interval?
(βj hat - t sqrt(s2vjj), βj hat + t sqrt(s2vjj)), where t is the 95% confidence statistic (for two sided test).
How to do prediction interval?
(y*hat - A, y*hat + A), with A = t s sqrt(x*‘(X’X)-1x* + 1), t is the 95% test statistic
What is the LS derivation?
What are the advantages and disadvantages of the Least Absolute Estimation?
What are the ideal 5 conditions/assumptions?
- The model is linear
- The n x k matrix X is nonrandom and has rank k (thus all columns are linearly independent)
- The n x 1 vector u has mean zero and variance σ2In
- The N x 1 vector u follows a multivariate normal distribution
- If we let Qn = X’X/n then Qn –> Q as n –> inf, where Q is finite and positive definite k x k matrix. (Asymptotic, thus not very important for us)
What is meant by significance and importance?
Often we can ignore small unimportant variables, although our estimation could then be slightly more biased, it often also gains precision.
Significance: how precisely we manage to estimate a parameter
Importance: the impact of the parameter on the total outcome.
What does the Crame-Rao inequality mean?
It says that the varaince of an unbiased estimator achieves the Cramer-Rao lower bound it is efficient.
