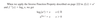Temple Precalculus Final All Flashcards
(138 cards)
1
Q
Definition of a Function
A
2
Q
2.1 Evaluating a Function Defined
A
3
Q
Four Ways to Represent a Function
A
- Verbal
- Visual
- Algebraic
- Numerical
4
Q
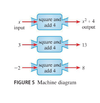
Function Machine Illustration
A
5
Q
Piecewise Function defined
A
6
Q
The Domain of a Function
A
7
Q
What about the domain of Radicals
A
Note if the radical is odd or even and the Bracket or parenthesis
8
Q
Absolute Value and Greatest Integer Function Graphs
A
9
Q
2.2 Equations that Define Functions
A
10
Q
2.2 graph of a piecewise defined function
A
11
Q
Graph of the Greatest Integer Function
A
12
Q
Linear Function Graph
A
13
Q
Reciprical Function Graphs
A
14
Q
Root Function Graphs
A
15
Q
The Graph of a Function
A
16
Q
The Vertical Line Test for Functions
A
17
Q
Definition of Increasing and Decreasing Functions
A
18
Q
Getting the Domain and range from a Graph
A
19
Q
Increasing and Decreasing Functions
A
20
Q
Local Maxima and Minima of a Function
A
21
Q
Power Function Graphs Exponents x^n
A
22
Q
Solving equations and Inequalities Graphically
A
23
Q
2.6 Even and Odd Function Defined
A
24
Q
2.6 Even and Odd Functions
A
25
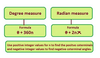
General Order of Operations
26
Horizontal stretching and Shrinking Graphs
27
Order of Operations when Evaluating Functions
28
2.6 Reflecting Graphs
29
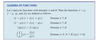
Algebra of Functions
30
Composition of 3 Functions
31
Composition of Functions
32
Composition of Functions Defined
33
Definition of the Inverse f a Function
34
**Dont Mistake the -1 in f^-1 for an exponent**
35
Finding the Inverse of a Function
36
Graphing the Inverse of a Function
37
Horizontal Line Test
38
Inverse Property Function
39
One to One
40
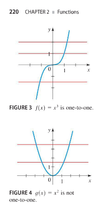
The Inverse of a Function
41
Arrow Notation
42
Definition of **Vertical** and **Horizontal Asymptotes**
43
**Difference of Squares is**
44
Finding **Horizontal Asymptotes**
45
Finding the **Intercepts** and **Assymptotes** and graphing them
46
Finding the **Veritcal** and **Horizontal Asymptotes**
47
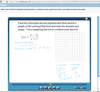
Finding the **x intercept**
48
Finding the **y intercept**
49
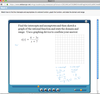
Findingthe **Vertical Asymptotes**
50
Graph of **f(x)=1/x**
51
**Horizontal Asymptote** with Translations
52
Transformation of a **Rational Function** y=1/x
53
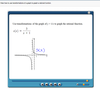
Transformations of the Graph of a Rational Function Stretching and Shifting
54
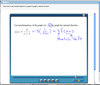
Making a Table to find the Intervals
55
Solving a Polynomial Inequality
56
Solving a Rational Inequality
57
Solving Polynomial Inequalities
58
Solving Rational Inequalities
59
**Compounded Interest** Formula
60
The Natural Exponential Function e
61
Graphing the Exponential Functions **e^x** and **e^-x**
62
Natural Exponent e^x graph transformations
63
**Continuously Compounded** Interest
64
The Number **e**
65
Common Logarithms
66
4.3 Definition of Logarithmic Functions
video
http://college.cengage.com/mathematics/blackboard/shared/content/video\_explanations/video\_wrapper.html?filename=kazmierczak/srwp60403a&title=Logarithmic%20Functions%20I
67
Definition of the Logarithmic Function
68
Graph of the Family of Logarithmic Functions
69
Graph of the Logarithmic Function
70
Graph of the Natural Logarithmic Function
71
Graphing a Logarithmic Function by Plotting Points
72
Inverse Function Property Domain
73
Inverse Property Function
74
Log to Exponential Form
75
Natural Logarithms
76
Omitting the Parenthesis
77
Properties of Logarithms
78
Properties of **Natural Logarithms**
## Footnote
**ln**
79
The Natural Logarithmic function is the inverse of the natural exponential function
80
Expanding and Combining Logarithmic Expressions
PG 355
81
Since Logarithms arw exponents the Laws of Exponents give Rise to the Laws of Logarithms
http://college.cengage.com/mathematics/blackboard/shared/content/video\_explanations/video\_wrapper.html?filename=kazmierczak/srwp60404&title=Laws%20of%20Logarithms
82
**WARNING** There is no corresponding Logarithm Rule for of a Sum or a Difference
pg 356
83
http://college.cengage.com/mathematics/blackboard/shared/content/video\_explanations/video\_wrapper.html?filename=kazmierczak/srwp70405&title=Compound%Interest
84
4. 5 Exponential Equation Inequality
https: //www.webassign.net/v4cgi/extra/bc\_enhanced/index.tpl?asset=watch\_it\_player&asset\_url=/bc\_enhanced/sprecalc7\_w\_player/scolalg5\_05\_04\_070.html&UserPass=40416dd1f85ab2d92f82bfef24bd5be5
85
http://college.cengage.com/mathematics/blackboard/shared/content/video\_explanations/video\_wrapper.html?filename=kazmierczak/srwp60405&title=Exponential%20Equations
86
4.5 Guidlines for Solving Exponential Equations
87
4.5 Solve the **Logarithmic Equation** for x
88
Solving an Exponential Equation by isolating the exponential term
89
Solving an Exponential Equation by isolating the exponential term
90
Using the Quadratic Equation to Solve a Logarithmic Equation
91
When an **exponential equation** is a **quadratic equation**
It must be **factored**
92
When the Exponential Equation has A Common Factor
93
When x is in the **denominator** of an exponential equation
94
When x is on both sides of the exponent
95
When x is on both sides of the exponent
96
4.6 Need Exponential Growth
97
get it from book problems pdf
98
Finding the Period of Sine and Cosine Curves
period=2π/k
99
Graph of the unit circle values
http://college.cengage.com/mathematics/precalculus/animations/stewart/sp060503f02.html
Note the color pattern as the circle stretches along the line as one period of 2π
100
Horizontal Shift on a Graph
Remember it is the part (x-b)
and is a shift in an **Unexpected** Direction
this affects x so it is in the parenthesis with x
101
One period of x=cosine t
0≤ t ≤2π
Graph of cos t for
0≤ t ≤ 2π
102
One period of y=sin t
0≤ t ≤2π
Graph of sin t for
0≤ t ≤2π
103
https://www.webassign.net/v4cgi/extra/bc\_enhanced/index.tpl?asset=watch\_it\_player&asset\_url=/bc\_enhanced/sprecalc7\_w\_player/sprecalc6\_05\_03\_043.html&UserPass=44b63ef21500978162e459f571f147ab
From the graph the period =2π
so
2π/k=2π
k=1
104
Periodic Properties of Sine and Cosine
Sine of t
or Cosine of t
remain the same as you ad 2π periods
105
Reflection of a Cosine Curve
Reflction of a cosine curve -cos
106
Vertical **Stretching** and **Shrinking** of a **Sin** Graph
**AMPLITUDE** is the **true Value** of the number in front of the **sin or cos**
⎢a⎥sin
The Higher the number the higher the peaks
y=2 sin x
Fractions cause Flatter Graphs
y=1/2 sin x
107
**Vertical** transformaton of Cosine Curve
**Vertical** transformaton of Cosine Curve by +2
108
The Cotangent graph does not cross the origin and swigs to the left
109
Periodic Properties of
tan
cot
sec
csc
110
The secant and cosecant period is 2π/k
111
Tangent and Cotangent figuring the period
π/k
112
Tangent Graph crosses the origin and swings to the right
113
The Cosecant Graph looks like a U between 0 and π in the first quadrant
with a period of π
and is an upside down U in quadrant 2
114
The secant graph has a period of 2π and looks like a U straddling the y axis
115
Inverse Cosine Function
116
Inverse Sine Function
117
Inverse Tangent Function
118
Angles in standard position all start (**initial side**) on the positive x axis
119
6. 1 Converting between Radians and Degrees
https: //www.webassign.net/v4cgi/extra/bc\_enhanced/index.tpl?asset=watch\_it\_player&asset\_url=/bc\_enhanced/sprecalc7\_w\_player/sprecalc6\_06\_01\_005.html&UserPass=bd5ee596620b98562a811b6665bca489
and
https://www.webassign.net/v4cgi/extra/bc\_enhanced/index.tpl?asset=watch\_it\_player&asset\_url=/bc\_enhanced/sprecalc7\_w\_player/sprecalc6\_06\_01\_017.html&UserPass=bd5ee596620b98562a811b6665bca489
120
Coterminal Angles-have the same initial and terminal sides just have more rotations of 360° or 2π
https://www.webassign.net/v4cgi/extra/bc\_enhanced/index.tpl?asset=watch\_it\_player&asset\_url=/bc\_enhanced/sprecalc7\_w\_player/sprecalc6\_06\_01\_035.html&UserPass=bd5ee596620b98562a811b6665bca489
**Positive** Coterminal Angles **add multiples** of **360°** or 2π
**Negative** Coterminal Angles **subtract multiples** of 360° or **2π**
121
Positive and Negative Angles are determined by the movement of the terminal side away from the initial side
clockwise-**negative**
**counter** clockwise-**positive**
122
How Radians (the preferred angle measure in calculus) are measured
Note the arc created by the line is the same length as the line or 1 radian
123
Trigonometry of right Triangles-
**The Special Two Triangles to Remember**
http://college.cengage.com/mathematics/blackboard/shared/content/video\_explanations/video\_wrapper.html?filename=kazmierczak/srwp70602&title=Trigonometric%20Ratios%20and%20Special%20
124
**Height** of a Building
Angle of **Elevation**
Angle of **Depression**
**Line of Sight**
125
Height of a Tree
126
Interactive Unit Circle
https://www.mathsisfun.com/algebra/trig-interactive-unit-circle.html
127
The **Reciprocal** Relations in Trig
## Footnote
**Cosecant**
**Secant**
**Cotangent**
128
SOHCAHTOA
129
The Unit Circle Cosine,Sine
130
The Trigonomic Ratios to Remember
131
Definition of Trigonomic Functions
132
Fundemental Identities of Trig
133
Reference Angle
134
**All** **S**tudents **T**ake **C**alculus
**All** **S**tudents **T**ake **C**alculus
135
**Reciprical** identities
**Pythagorean** Identities
**Even Odd** Identities
**Cofunction** Identities
136
Addition and Subtraction Formulas
137
Double Angle Formulas
138
