SWE Flashcards
SWE: What does it mean for function f(n) to be big-O of g(n), or f(n) in O(g(n)), or f(n) = O(g(n))
There exists number n* and constant c so for all n > n*,
f(n) < cg(n)
SWE: At a high level, what does it mean for f(x) to be big-Omega of g(x)?
It means g(x) is big-O of f(x); it reverses the relationship.
What type of bound does big-O provide on the runtime of our algorithm? What about big-Omega? What about big-Theta?
Big-O provides an upper bound
Big-Omega provides a lower bound
Big-Theta provides both an upper and lower bound, or a tight bound
SWE: What does it mean for f(n) to be big-Theta of g(n)
f(n) is both big-O of g(n) and big-Omega of g(n)
SWE: When we use big-O, are we typically describing best-case, worst-case, or expected-case run time?
Worst case. (But it can be used for the other two.)
SWE: What does asymptotic analysis do for function f(n)? What is our primary tool for asymptotic analysis?
It describes the limiting behavior for function f(n). We use big-O.
SWE: If we have two arrays with lengths a and b respectively, what is big-O run time for nested loops iterating through all elements of one array for all elements of another?
O(ab)
SWE: What are the two main rules for calculating big-O of a function f(n)?
Drop any constants, either multiplicative or additive, and drop any additive terms that are asymptotically not the largest.
SWE: What is big-O of f(n) = 4*2n + 3n10 + 10?
O(2n)
SWE: What “general pattern” emerges for O(log n) runtimes?
Continually dividing n by some constant, such as 2, until you reach 1. (Or, continually multiplying a constant by another constant until you reach n.)
SWE: Why can string questions be approached as array questions, and vice versa?
Because a string is just an array of characters.
SWE: What is a (singly) linked list?
A list of nodes, where each node has a value and a pointer to the next node.
SWE: What is a double linked list?
A list of nodes, where each node has a value and a pointer to both the previous and next node.
SWE: What is an advantage of linked lists over traditional arrays? What is a disadvantage?
Advantage: You can add and remove elements from the end of the list in constant time (whereas with a resizable array, additions are only amortized constant time)
Disadvantage: You can no longer use an index to find a value in constant time. If you want the kth element, you must iterate through k nodes.
SWE: In a linked list, what is a null node, and what is is used for? (In 122’s particular implementation, which I’ll use)
It is a note with a null data value and a null pointer to the next node. It serves as the end of the linked list, or the final node. When iterate throught he list and find a null node, we know the list is over.
SWE: In a linked list, what is a root node?
The root node is the current first node.
SWE: How would we draw a 2 element linked list, where we have 3 nodes: a root node, a normal node, and our null node?

SWE: When we add a node to a linked list, and the linked list is drawn in our typical way, do we add the node to the left or the right? Why?
The left!
SWE: How do we add a new node to a linked list?
Set the new node to be the root node, and set the pointer of the new node to go to the old root node.
SWE: How do you implement a linked list in python, with add and remove methods?

SWE: Are linked list problems commonly recursive or iterative?
Recursive, because linked lists have a naturally recursive structure. (But there are many problems with iterative solutions too!)
SWE: What is the runner technique for linked lists?
You examine the linked list using two pointers: one that is “slow”, and one that is “fast” and is generally at a farther position in the linked list, and which moves faster than the other.
This is a pretty general technique, but be aware that it exists: examining with two pointers might be handy for many problems.
SWE: What is a hash table used for, and what makes it so useful?
A hash table is a data structure that maps keys to values; you insert key-value pairs, and then search for a key to get its value.
It is useful because it enables fast lookup of elements, in basically constant time as long as your hash table has enough available memory.
SWE: What Python data structure implements the hash table?
Dictionaries (or defaultdicts, which are convenient)
SWE: How is a hash table implemented? What components are needed, and how are they used to insert a key-value pair, or retrieve a key-value pair? (There are multiple possible implementation strategies, we just focus on one in particular.)
Our hash table is an array of linked lists. So each entry in the array is its own linked list.
We use a hash function to map keys to an entry in the array, and this mapping is used for both insertion and retrieval.
To insert pair (key,val), get your hash value h(key), and then find your array index using h(key)%m, where m is the length of the array. We use modulus to keep the index within bounds. We then add our (key,value) pair to the linked list: if the key is already there, we update the value; otherwise, we add a new node with that key-value pair.
To check the value for a key, we get our index h(key)%m again, and look for our key in the linked list at that index. If it isn’t there, then that key hasn’t been inserted.
SWE: What is a hash function? What in general makes a “good” hash function in the context of, say, a hash table?
A hash function maps some value to an integer, in a non-random way. A good hash function will “evenly distribute” values across the different integers. In the context of a hash table, it should distribute the integers evenly across each of the cells of the array. This is good because it leads to fewer long chains in the hash table.
SWE: When making a hash table, why do we need a linked list in every cell? Why can’t we just insert key-value pairs into the cell directly?
Because of collisions: if 2 pairs are mapped to the same cell, they collide, and we can’t put them both in the same cell. Hence, a linked list is used.
SWE: When discussing hash tables, what is a load factor? What does it describe
The load factor is the number of keys in the hash table divided by the length of the array. It is n/m.
It describes how “full” the array is, or how long on average the chains are: if you have a load factor well over 1, then you have several collisions and longer chains.
SWE: What is the worst-case runtime for a lookup in a hash table, in terms of the number of keys n? In what sorts of situations would this happen, and how do these situations cause this runtime?
The worst-case runtime is O(n). This would happen if your array isn’t large enough, and as a result you have some long chains in some of the array indexes.
When looking for a key in a chain, it is O(k), where k is the number of keys in the chain. If you have a lot of keys in the chain – an amount that becomes substantively “on the order of” n, such as say n/10, then you’re looking at linear time.
SWE: When using a hash table, how can we assure constant-time insertion and lookups?
You need to keep your load factor low; you need to have a large enough array so there are few collisions, leading to chains that are at most a few elements long.
SWE: Hash tables are typically used for storing (key,value) pairs, but what is an intuitive way to have them store just keys? So like a set in python rather than a dictionary?
In traditional hash tables, you hash the key, then insert the key-value pair at the corresponding location. But there’s no reason you need a value: you could just insert the key.
(If you have a hash table set up like a dictionary, you could also just give every key a value of NULL which you ignore.)
(This is pretty simple, but I want to remember you can also easily make a hash table that works like a set!)
SWE: Is a stack first-in-first-out or first-in-last-out? Is a queue first-in-first-out or first-in-last-out?
A stack is first-in-last-out
A queue is first-in-first-out
SWE: What is a stack? How is it used at a high level?
A stack is a data structure which stores elements. You can add an element (or “push” it), and you can remove an element (or “pop” it). Elements are removed in reverse order of how they’re added, or first-it-last-out. This is like a stack of blocks where you continually add a blocks to the top when you want to add, and remove a blocks from the top when you want to remove.

SWE: How do you simply implement a stack – with pop, push, peek and isEmpty methods – if you already have an implementation of another key data structure?
You need a linked list implementation. Recall that a linked list has a null node as the “final node” on the right with no descendants, and the “first node” being the root node which has nothing pointing to it. To add an element to the linked list, you make it the root and make the old root its descendant. To remove an element, you make its descendant the root.
In other words, a linked list is basically already an implementation of a stack. To push, you just add the value to the LL. To pop, you just remove the root from the LL. To peek, you just look at the value in the root of the LL. To check if it’s empty, you see if the root node is the null node.
SWE: What is a queue? How is it used at a high level?
A queue is a data structure which stores elements. You can add an element (or “push” it), and you can remove an element (or “pop” it). Elements are removed the same order as how they’re added, or first-it-first-out. This is like a queue of people who are waiting in line, where the first person to get in line is the first person to get out.
SWE: How do we implement a queue, with push, pop, peek, and isEmpty, using another common data structure?
We will implement the queue using a slight variation of a linked list.
With a normal linked list, the list is visualized several nodes with arrows pointing left to right. On the far left is the root node; the linked list data structure keeps track of the root node, and a newly inserted value enters on the left and becomes the new root. The linked list also has a null node to the far right.
In a queue, we are going to insert elements on the right side of the linked list, or the back, and we (same as a normal linked list) remove elements from the left side of the linked list, or the front. So the arrows between nodes point from front to back, which may seem unintuitive.
Thus, we now keep track of two nodes rather than just one. We keep track of the front, or the root, as well as the back, which is the last node in the list. The back node doesn’t point to anything; it’s easier in a queue to not have a null node and instead keep an “empty” bool in the data structure. When the queue’s empty, set the front and back pointers to just point to NULL.
To push a value onto the back of the list, we make a new node, have the current back point to it, and set the new node as the back. To pop a value from the list, we set the front’s descendant as the new front. To peek, we return the value at the front. For isEmpty, we check the bool.

SWE: What is a tree?
A tree is a data structure which organizes nodes in terms of parent-child relationships, where each node can have at most one parent, but nodes could have several children.
A tree is basically a DAG, or directed acyclic graph, that is also connected, meaning it’s not like two or more graphs that don’t touch each other.

SWE: In a tree, what is a parent and what is a child?
Simply, if node A is directly above node B, A is the parent of B and B is the child of A
SWE: In a tree, what is an ancestor and what is a descendant?
A descendant of node A is any node you can get to by following branch down from A.
An ancestor of A is any node for which A is a descendant.
SWE: In trees, what is a branch, starting at say node A
A branch is a “path” from start node A down through multiple parent-child relationships, always moving from parent to child, until we reach a leaf node.
SWE: In trees, what is a leaf? What is the root?
A leaf is a tree with no descendants; the root is a tree with no parents.
SWE: Given a tree, what is the subtree with node A as the root?
It’s simply all node A as the root of a tree with all of the descendants. It’s basically the tree you get if you erase anything from the original tree that wasn’t A or a descendant of A.
SWE: What makes a tree binary? What makes a tree ternary?
A binary tree is where each node can have at most two descendants (but only 1 parent). A ternary tree is where each node can have at most three descendants (but only 1 parent). And so on.
SWE: What is a binary search tree?
It’s a binary tree where, for every node n, you have the property that:
All left descendents of n < n < all right descendants of n.
(There can be differing opinions on equality in the tree. Sometimes above will read <= n
SWE: How do you search for an element in a binary search tree? How do you insert a new element into a binary search tree (where it doesn’t necessarily need to be balanced)?
To search for an element x, you follow a branch down the tree using the information that the tree is in a way “sorted”. So if you’re at node y and y < x, you move down the left branch, because x then would definitionally need to be on the left. If x < y, you move down the right branch.
To insert, you do the same thing and move down the tree in this way. If you find x, you typically wouldn’t insert it again. If you find a leaf without finding x, you insert it on the appropriate side of the leaf.
SWE: Why is a binary search tree useful for searching for elements?
Because of the ordering properties of the BST, you only need to search down one branch rather than the whole tree. This means that if the tree is balanced, you can search for an element in only log(n) time.
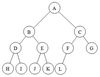
SWE: What is a complete binary tree?
A complete binary tree has every level fully filled out, except for potentially the last level. If the last level isn’t full, it’s filled in from left to right.
SWE: What is the height of a tree? What is the height of a tree with just a root, or an arbitrary tree?
The height of a tree is the length of its longest branch. Specifically, it’s the number of edges along the longest branch.
We say that just a root node has a height of 0, because the longest path has no edges.
To find the height of an arbitrary tree, just follow all the branches down to their leaves, adding 1 to that branch’s length for each node past the root, and thus for each edge. Take the max branch length as the height.
SWE: What is one way you learned to achieve balanced binary trees?
AVL Trees
SWE: What is the technical definition of a balanced tree? And what is a more colloquial, slightly more relaxed definition of a balanced tree?
Technically, a balanced tree is a tree such that, for every subtree present, the height of its left subtree and its right subtree differ by at most 1.
Colloquially, it’s basically a tree that is balanced “enough” among all subtrees such that we can expect traversals of a single branch to take O(log n) time, rather than linear time.
SWE: How do you implement a tree where each node can have an arbitrary number of descendants? What datatype is necessary, and what datatype is optional but usually not useful for interviews?
Also, how would you adapt this implementation to be specifically a binary tree?
You will need a treeNode class, which has a data attribute holding its value and a descendants attribute which holds a list of its descendants.
You can also include a Tree class, whose only attribute is a root node, but it’s usually not helpful for interviews?
If you want specifically a binary tree, your treeNode class would have three attributes: data, leftDescendant, and rightDescendant.
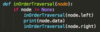
SWE: What is an in-order traversal of a binary tree? How would you write a function to perform an in-order traversal of a binary tree, which takes a root node as input and prints a node’s data whenever it “visits” that node?
In an in-order traversal, at every node, you explore the left subtree of the node (and visit all of the nodes in that subtree), then visit the node itself, then visit all of the nodes in the right subtree.
A recursive function is as follows, which implicitly handles the base case by doing nothing if we’ve reached a null node:
SWE: What is an pre-order traversal of a binary tree? How would you write a function to perform an pre-order traversal of a binary tree, which takes a root node as input and prints a node’s data whenever it “visits” that node?
In an pre-order traversal, at every node, visit that node, then you explore the left subtree of the node (and visit all of the nodes in that subtree), and then visit all of the nodes in the right subtree.
A recursive function is as follows, which implicitly handles the base case by doing nothing if we’ve reached a null node:

SWE: What is an post-order traversal of a binary tree? How would you write a function to perform an post-order traversal of a binary tree, which takes a root node as input and prints a node’s data whenever it “visits” that node?
In an post-order traversal, at every node, you explore the left subtree of the node (and visit all of the nodes in that subtree), then visit all of the nodes in the right subtree, and then lastly you visit the node itself.
A recursive function is as follows, which implicitly handles the base case by doing nothing if we’ve reached a null node:

SWE: What is a max heap, in the context of a min heap? Why is it very easy to implement a max heap if you understand min heaps?
In a min heap, all nodes’ descendants are larger than the node. For a max heap it’s simply the opposite: all nodes’ descendants are smaller, so the max is at the top. So the implementation is basically the exact same, you just do the orderings in reverse.
SWE: What is a binary min-heap?
A complete binary tree where each node is smaller than its children, so the min of the tree is always at the root.
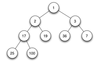
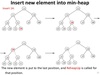
SWE: How do we insert a new value into a min heap?
A heap must be a complete tree, meaning the bottom layer is filled out from left to right; so, we start by placing our new node in the bottom layer, to the right of the rightmost node in that layer.
Then, we continually swap that new node with its parent, until its parent has a lower value than it. This restores the min heap to its correct form.
SWE: How do we extract the minimum value from a min heap, removing it from the tree?
We first remove the minimum value from the top (it’s always at the top).
A min heap must be a complete tree, so next we take the rightmost node on the bottom layer and place it at the top, where the min value originally was.
Now we need to restore the ordering. We continually look at the node we just moved to the top and its two descendants. If the node we moved is the smallest of those three, we stop. Otherwise, we swap it with whichever of its descendants is the smallest of the three.

SWE: What is the time complexity of inserting a new element into a min heap, and why?
When inserting a new element, we put it at the bottom so as to preserve the completeness of the tree, then swap it up a branch until the ordering condition has been restored. Because the tree is complete, it is balanced, and so the branch is at most O(log n) in length. Thus we have an O(log n) solution.
SWE: Is a complete tree always balanced? Is a balanced tree always complete?
A complete tree is always balanced.
A balanced tree is not always complete.
SWE: In a min heap, what is the time complexity of just checking the min element, but not removing it?
Constant time: it’s always at the top.
SWE: What is the time complexity of extracting the min element from a min heap, removing it from the tree? And why?
When removing the min element, you take an element from the bottom level and put it at the top where the min element was, then swap it down a branch until the ordering condition is restored. Because the min heap is a complete tree, it is balanced, and so the branch is at most length O(log n). Thus, it’s an O(log n) algorithm.
SWE: Why are min heaps (or heaps in general) useful? Why are they sometimes called priority queues?
A min heap is somewhat fast to maintain, as inserting an element takes O(log n) time, and you can always find the min element in constant time. Also, removing the min element takes only O(log n) time.
This means that you always have the “most important” or “most pressing” element in the heap ready to go at a moment’s notice. This gives the name priority queue: drawing from a queue returns elements, and this one does so in order of priority, as several draws will yield the highest priority elements, in order. This would be useful in a hospital, for example, as we want to continually admit the patient in the most critical condition.
SWE: What is a priority queue another word for?
A heap.
SWE: At a high level, what is a trie (or prefix tree), and what is it typically used for?
A trie is a tree with a letter at each node. As you move down a branch, you find a word, or a prefix for a longer word.
Branches sometimes have * values at the leaves to signify the end of a word.
They’re often used for interview problems where you need to look up words, or several words with the same prefix, etc. You can see if a word is present in the trie in O(length of word) time, because you can follow the prefix down the tree.
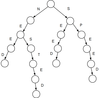
SWE: What two things define a graph?
A list of nodes (or vertices), and a list of edges connecting those nodes.
SWE: What is a directed graph? An undirected graph?
In a directed graph, the edges have arrows from one node to another. In an undirected graph, the edges don’t have arrows, and count as going in both directions?
SWE: What is a graph path?
A sequence of vertexes connected by edges. For directed graphs, a path must follow the arrows.
SWE: What is an acyclic graph?
A graph where no node has a path out and back to itself.
SWE: What are the two most common high-level ways to implement a graph?
Adjacency list, and adjacency matrix.
SWE: What is an adjacency matrix for a graph?
An adjacency matrix is one way to store a graph in memory.
For a graph with n vertices, an adjacency matrix is an nxn matrix, where the ijth entry is a 1 if there is an edge from i to j, and a 0 if not.
For undirected graphs, the matrix is symmetric, because an edge from i to j also goes from j to i.
SWE: What is an adjacency list?
An adjacency list is one way to store a graph in memory.
For each of your n nodes i, you have a list of the nodes j for which there is an edge from i to j.
(If your graph is undirected, there will be some redundancy in your adj. list, as each edge needs to appear twice.)
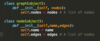
SWE: How would you implement an adjacency list for a graph in an object-oriented way? How would you implement it just using list data structures?
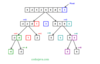
To do it object-oriented, you could have a Graph class, with objects having a list of nodes as an attribute, as well as a Node class, with objects having a name attribute as well as a ListOfEdges attribute, which is just a list of the nodes into which it has an outgoing edge. The picture shows this implementation.
To do it with just arrays, you could assume your n vertices are indexed from 0 to n-1 and use a 2d list: each entry at position i in the high-level list would be a list of indices j into which i has an outgoing edge.
SWE: What are some advantages of adjacency lists over adjacency matrixes when representing graphs? Disadvantages?
An adjacency list only needs to store the edges that do exist, whereas an adjacency matrix stores an entry for each possible edge from i to j. Adjacency lists are thus more space efficient, especially if the graph is sparse.
With an adjacency matrix, you can check for an edge in constant time; for an adjacency list, you need to iterate through all of the edges in one of the nodes, taking O(# neighbors) time.
Conversely, with an adjacency list, you can get a list of out-neighbors in constant time, which is useful for things like searches from A to B. In an adjacency matrix, you need to iterate through all possible neighbors to see which are actually neighbors.
SWE: What is Depth-First Search, or DFS? How does it work at a high level?
Depth-first search is a way of searching through a graph, to either visit all of its nodes, or to find a specific node. In depth-first search, you move fully down a branch before moving to the next one, hence “depth-first.”
A depth-first search starts at a specific node in the graph; you may be given a specific start node, or it may be arbitrary. You search through each of the node’s neighbors, but you move fully down a branch before moving to the next. You must keep track of all of the nodes you have visited, because if you see a node you’ve already visited while exploring a branch, you don’t visit it again.

SWE: What is some pseudocode for depth-first search?
A recursive approach works best:

SWE: What is Breadth-First Search, or BFS? How does it work at a high level?
Breadth-first search is a way to search through a graph, in order to either traverse all of the nodes, or to find a path from one node to another. You’re given a starting node (or choose one randomly), and then you visit all of its neighbors before visiting any of their neighbors, hence “breadth-first.” You can think of it as moving out from the root layer-by-layer.

SWE: What crucial data structure should be used for implementing breadth-first search?
A queue
SWE: What is some pseudocode for breadth-first search?
We use an iterative solution (unlike DFS, which is recursive) which takes advantage of a queue. The queue stores nodes we need to visit, in the order in which we need to visit them.
We “mark” a node before pushing it onto the queue, and when iterating through a node’s neighbors, we only push it onto the queue if it isn’t marked. This is because we always push a node on after we mark it, so if it’s already market, that means it’s already in the queue, and we don’t want to put it in the queue twice and thus visit it twice.

SWE: How does bubble-sort work at a high-level? Additionally, how do you code bubble-sort in Python?
Bubble sort sorts the elements of a list by continually finding the largest element and moving it to the end of the list. So you find the largest element and put it last; then you find the second-largest element and put it second-last; and so on. You do this by continually passing forward through the list and switching an element with the next element if it’s larger than the next element.

SWE: What is the time complexity of bubble sort for a list of length n? How much memory does it require, not including the original array?
Time is O(n2), Space is O(1).
SWE: What is selection sort? How does the algorithm work?
You sort an array by scanning through the whole array, finding the smallest value, and moving it to the front; then, you scan through the final n-1 elements and move the smallest remaining element to the second position; and then the 3rd smallest element from the remaining elements; and so on.
SWE: What is the time complexity of selection sort for a list of length n? How much memory does it require, not including the original array?
Time is O(n2), Space is O(1).
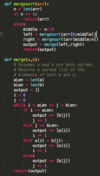
SWE: How does mergesort work at a high level? How do you code it in Python?
You split the array into two halves, sort those halves recursively, and then combine them using a merge() function, which can combine two sorted lists into one sorted list containing the elements from both. Your base case is if a list has length <= 1.
To merge two lists, just continually add the smallest element in either list to a helper list, with pointers in each list keeping track of which elements you’ve already viewed?
SWE: What is the time complexity of mergesort (for an array of length n), and why? What is the space complexity, and why?
The time complexity is O(n log n). Here’s how to think about this: we split the array into singles; then we merge into doubles, then quadruples, etc. In order to merge two lists, we need to traverse both lists. So when combining singles into doubles, we must traverse each single once; when combining doubles into quadruples, we must traverse each double once; and so on.
This means that at every “level”, we need to traverse all the data. And how many levels are there? We merge 1’s, then 2’s, then 4’s…up to n. So log n levels, each traversing the whole dataset of length n, gives O(n log n).
The space complexity is O(n). We need to store temporary arrays to fill with the sorted values, and the max length of one of these arrays is n. We can reuse the same space for each array assuming we are solving the problem with a single processor, and thus only working with a single recursive example each time. Thus, O(n) space.

SWE: How does quicksort work? How does the algorithm work at a high-level? And how do you code it in Python?
It’s recursive: if the length of the list is <= 1, you just return the list.
Otherwise, you pick a “pivot”, which is just any of the elements of the list. You could pick it randomly (preferred), or have some default like always picking the first element in the list.
Then you move through the list, putting each element in one of 3 new lists: less than the pivot, equal to the pivot, and greater than the pivot.
Lastly, you recursively sort the elements on either side of the pivot, then you combine the lists.

SWE: What is the worst-case runtime of quicksort? What is the average-case runtime of quicksort? And why?
The average-case runtime, or the expected runtime, is O(n log n). This is because on average, the element you choose as the pivot will equal about the median of the list. So you split the list into roughly equal parts, then recurse and split the sublists into roughly equal parts, etc. So we now have a setup that looks a lot like mergesort: you have log n levels, and at each level you handle each element in the original list once, giving O(n log n).
The worst-case runtime is O(n2). If you always pick the biggest element in an array as the pivot, for example, then your splits of the list are always uneven, and you sort lists of size n, n-1, n-2… as opposed to n, n/2, n/4….. and this leads to O(n2).
SWE: Have I learned the space complexity of quicksort yet?
Nope, I don’t know, it’s weird and complicated and different in different sources. May want to look it up.
SWE: How does radix sort work?
Radix sort sorts an array of numbers using their individual bits, or individual digits.
First you sort the list based only on the first digit (meaning the lowest digit), and you maintain the original order if the first digits are equal. So [3,9,0,6,33,23] becomes [0,3,33,23,6,9].
Then you sort by the only the second digit, and you again preserve ordering if the second digit is equal. This means that now they will be sorted based on the last two digits: because we’re sorting based on the tens place second, it takes precedent; but, within numbers with the same tens digit, the ones digit is implicitly used to make further distinctions, as we already sorted by it earlier.
Then we sort by the 100’s place, then 1000’s, and so on until all digits have been used.
https://www.youtube.com/watch?v=XiuSW_mEn7g
This shit is crazy.
SWE: What is the runtime of radix sort? And why?
O(kn), where n is the number of elements in an array, and k is the max number of digits of an element in the array.
We need to do k sorts: first by the one’s place, then the ten’s, all the way up to the largest digit that’s present. But how long does each sort take? Well, if we’re working in base 10, and we only look at one digit in each number for each sort, then there are effectively only 10 unique numbers in the list during any of the sorts.
This means that each of the sorts can be done in O(n) time. I’m not sure the most elegant way to do it, but here’s one way that works: for base 10, just create 10 lists, with one for each digit. Pass through the list, and add each element to the list with the relevant digit. Then just append all 10 lists, and you’re done. Because we have a constant number of lists, or a constant number of possible values, we can do a sort in O(n) time.
Thus, we have k sorts of time O(n), for O(kn) runtime.
SWE: When is radix sort useful, and why is it useful in this case?
It’s useful when we have a lot of numbers in the list, but all of the numbers are small, or have a small number of digits.
This is because radix sort takes O(kn) time where k is the max number of digits for an element, whereas other sorting algorithms take at best O(n log n) time. So if k is significantly less than log n, radix sort will be faster; and k will be significantly less than log n if there are lots of numbers, but they’re all small numbers.
SWE: How does binary search work?
You are searching for an element in a sorted array.
You basically continually divide the array in half. You look at the middle element, and if it’s larger than the target element, you search in the half of the array below the middle; if the middle is smaller than the target element, you search in the half of the array above the middle; and if you found it you’re done. You recurse like this, and if you run out of list, then it’s not there.
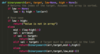
SWE: How do you write binary search in Python?
SWE: What is the runtime of binary search? When is binary search useful, and what prep do you need to do to run it if you want to use it in this case?
Binary search is O(log n) if you have a sorted list, otherwise you can’t run it.
Binary search is great if you’re searching the same list for elements over and over again. In this case, you sort the list first, which takes O(n log n), then you can make lots of searches all at O(log n). If you didn’t sort, you would save that O(n log n) cost, but all of your searches would be O(n) each.
SWE: What is a good hint that an interview problem may have a recursive solution?
If we’re computing n of something; often times we can compute the nth given the n-1th, and this lends itself to recursion
SWE: For recursion, what are the three most common high-level ways to divide a task with n parts into recursive sub-problems we can solve?
- Top-down: start by figuring out out how to solve for the nth by calling your function for the n-1st value, and solve that using the n-2nd, and so on.
- Bottom-up: figure out how to first solve for your first value, then use that to find your second, and on up until you reach n.
- Figure out how to divide the problem of size n into two problems of size n/2, as with merge sort.
SWE: How to recursive solutions typically compare to an iterative solution to the same problem in terms of space efficiency, and why?
Recursive solutions are often much more space inefficient than iterative solutions.
Say we’re generating n numbers. In an iterative solution, we probably generate the first, then the second, then the third, and once we’re done with a number, we can reuse the space that computed it for the next.
Conversely, if we have a recursive solution where we base the nth number on a call for the n-1st number, and base that on a call for the n-2nd number and so on, all n calls must be in memory at the same time. This can often lead to O(n) space (or even worse), when the iterative solution may have worked in constant space.
SWE: What is a helpful trick for figuring out the runtime of a recursive algorithm?
Drawing a tree of the recursive calls, then trying to figure out how much runtime each of the calls in the tree takes on average.
SWE: In the context of recursive algorithms, what is memoization? Why is it useful?
Sometimes in recursive algorithms, we need to solve the same subproblem more than once. An example of this is fibonacci numbers: because f(n) builds on two different subproblems via f(n) = f(n-2) + f(n-1), the tree may have a ton of repeats, and this can cause giant slowdowns in memory (recursing fibonacci takes exponential time).
To solve this, we use memoization, which simply means whenever we calculate the answer to a sub-problem, we store the answer, in something like an array or a hash table (more often hash table in my experience). And whenever we go to calculate a sub-problem, we first check to see if the answer is already stored, in which case we can just pull the answer.
This means we onle need to calculate every subproblem once, which greatly helps runtime (memoizing fibonacci numbers using an array, for example, brings the runtime down to O(n)).
SWE: How does bottom-up dynamic programming work?
When calculating a big value recursively, we start at the beginning with the base cases, and work our way up the recursion, storing the answers to progressively larger values until we get to our target. We can store the answers in an array or, more commonly in my experience from classes like 210, a 2d-array.
SWE: What are the two main structures in a computer’s memory for storing variables?
The stack and the heap
SWE: In computer memory, what is the stack? How does it work, and what types of things does it store?
The stack is a device in computer memory that stores local variables for your function calls. It is also a literal stack: whenever you create a local variable during a function call, it is pushed onto the stack; whenever you need to access a variable in the stack, we find it presumably by popping elements until we get the one we need, then putting everything back in.
It is also a temporary memory storage; when your function call ends, all of the local variables from the function call are popped off the stack and lost forever. Because of this, you don’t need to worry about deleting things from memory yourself; the computer handles garbage-collection automatically for the stack.
SWE: In computer memory, what is the heap? How does it work, and what types of things does it store?
The heap stores global variables which can be accessed by any function, i.e. with global scope. In order to write to the heap, you must use a function like malloc() or calloc(). To access something on the heap, you need a pointer to it.
On the heap, garbage collection is not handled automatically for you. You must take care to delete values when you are done using them, otherwise you’ll have a memory leak.
SWE: What are some pros and cons of using the stack vs the heap to store variables?
The stack has very fast access, and you don’t have to worry about memory leaks. However, variables on the stack can only be accessed within the function call that createed them, and on most CPUS the stack has a memory limit that is much less than the heap.
SWE: What is the difference between malloc() and calloc() when allocating memory on the heap?
Malloc takes one argument: the number of bytes that must be allocated.
Calloc takes two arguments: the number of objects that must be allocated, and the size of each object in bytes. It then calculates the total number of bytes needed by multiplying.
So malloc is marginally faster, but calloc is a bit more intuitive to use as a programmer.
SWE: At a high level, what will an object-oriented-design interview question often look like?
You’re given a situation that contains a variety of different objects, as well as relationships between objects, and processes involving these objects. You will need to design an object-oriented framework that will represent these objects/relationships and carry out these processes
For example, say you need to do represent a restaurant. You’ll have objects like customers, tables, servers, and orders, with servers having their customers, and processes including seating guests, taking orders, paying for food, etc.
These questions will often involve a fair amount of ambiguity. It will be up to you to brainstorm the most important objects, relationships and processes, as well as ask the interviewer for clarification on the use case and its key elements.
SWE: In OOP, what is a class and what is a subclass? Why is the use of subclasses useful?
A class is an object types, and subclasses are just specific subsets of that object type. If B is a subclass of A, then every instance of B is an instance of A, and we can do A-related operations on instances of B, but not vice-versa.
For example, maybe we have a Vehicle class, and we have Truck, Car, and Motorcycle subclasses. An instance of any of these subclasses is still an instance of Vehicle, and we can still get Vehicle attributes like mpg, top speed, etc. But the subclasses also have additional information: maybe Truck has truckbed_size, or Motorcycle has gang or something.
Subclasses for one allow us not to retype lots of code. Rather than saying that each of Truck, Car and Motorcycle have an mpg attribute (or a common method), we say that Vehicle does, and then they all inherit it. Inheritance decreases duplicate code.
The class-subclass system allows us to keep track of similar objects, while also giving needed attributes to individual object types, in a neat and intuitive way.
SWE: In Python, what two methods do I need to give a custom class in order to add instances of it to sets and dictionaries? How do you implement these at a high level?
__hash__(), and __eq__()
So you need to be able to hash an instance, and check if an instance is equal to some other variable.
For hashing, we typically hash one of the instance’s attributes. If class A has a field A.id, we might say
__hash__(self): return(hash(self.id))
For equality, we first check if the other object is an instance of class A, then we check equality of one or more fields to see that the instances are equivalent. (if we don’t check isinstance, we might draw an attribute from a datatype that doesn’t have that attribute, causing an error):
__eq__(self,other) =
return(isinstance(other,A) and self.id == other.id)
SWE: In Python, how do I make a class A with attribute x, and a subclass B that has attributes x and y? Both classes should have __init__() functions

SWE: In python, if you have a class A with several methods, and you make a subclass B via “class B(A): …”, how do you get all of A’s methods to work for B as well?
This happens automatically. You can just write
“class B(A): pass”
and you would have a subclass B with all the functionality of A.
SWE: In Python, if we have a class A and a subclass B, how do we override the method g() from class A, so that “g” has a different functionality in subclass B?
Simply redefine g() in subclass B. If you don’t specify a g() when creating subclass B, it’ll use class A’s g(), but if you do specify a g(), then that is what will be used.

SWE: In Python OOP, what method do we need to implement to be able to print our custom class A?
__repr__(self)
SWE: In Python OOP, when we have class A with method f(), do we call it on instance a with a.f(), or f(a)?
a.f()
This is kinda obvious, because it’s a method, but just remember this.
SWE: What is a seven-step process for answering a data structures/algorithms interview question?
- List carefully for any unique information about the problem (i.e. maybe the list is sorted, or maybe your algorithm is run many times), and ask any necessary clarifying questions.
- Draw and think through a specific example, which is large enough to think through the problem and is not a special case.
- Talk through a brute-force solution to establish a baseline, but don’t code it up. Also explain baseline time and space complexity.
- Find a better algorithm, through speaking and consideration. Will expand on this in other cards.
- Walk through the algorithm again to make sure you understand it and can code it effectively. Potentially use brief pseudo-code here.
- Code your solution elegantly, with good style. Start in top-left of board and write neatly, modularize code as much as possible, use good variable names but potentially abbreviate long ones after 1st use. Also, keep a list of things to improve or test as you code.
- Test your code and iteratively improve it. Read through lines, and look for weird-looking code as well as code that tends to cause issues (base cases in recursion, integer division, etc). Then, try small test cases you can get throug quickly, as well as edge cases.
SWE: What is the BUD technique for optimizing your solution to a programming problem/interview problem?
BUD is perhaps the most important method for figuring out how to improve your existing solution. It stands for Bottleneck, Unnecessary Work, Duplicated Work. You look for these things, in this order, and try to make them faster or better.
Bottleneck: Identify the part of your algorithm that is costing the most in terms of time complexity, or find the part that is “causing the big O to be what it is.” If your algorithm is to first sort an array in n log n time, and then to search for an element in log n time, then there’s not buch use trying to optimize the searching part: the first step of sorting is the bottleneck, so try to fix this.
Unnecessary Work: Find work your algorithm is doing, or can do in certain instances, that isn’t contributing to finding a solution. For example, maybe your algoritm is iterating through a list, and it could stop the iteration when it finds the answer in the middle, but doesn’t: here you should institute a break condition in the loop to avoid unnecessary work. Or, maybe your algorithm is iterating through all possible triples to solve an equation like a+b+c = 0, when it could just iterate through pairs, and then check the only possible value for the remaining number c. Look for things like that.
Duplicated Work: Maybe your brute force/nested loop solution checks the same possible answer twice, or performs the same process twice because it occurs in two different parts of the problem. Look for these and figure out how to only do work once: maybe you memoize, or otherwise come up with a system.
SWE: What are some other methods for finding a better, more optimized solution to an interview problem? (4 methods)
DIY (do it yourself): Walk through another example, maybe one that’s a bit bigger, and rather than thinking about computery and algorithmic jargon, just try to solve the example in the way your human brain intuitively does it. Often you default to something that’s pretty good, so turn your brain off and see what that default is.
Simplify and generalize: Try to solve a simplified, easier version of the problem, and then see how the ideas from that simplified version can be applied to the original problem.
Base case and build: First, just solve the problem for an instance that is “size 1”, whatever that means for your problem. Then, try to solve it for “size 2”, then “size 3”, etc. As you do this, try to find ways to use your size 2 solution during size 3, or use size 3 during size 4, or wherever you can see it work. This can lead to a good recursive solution.
Data structure brainstorm: Run through a bunch of data structures (array, hash table, heap, sorted list, tree, graph, linked list, etc) and try to think of how you could apply it. Maybe one of them has the runtime you’re looking for for a particular action, etc.
SWE: What is BCR, or best conceivable runtime?
For a given task, best conceivable runtime is a runtime or big O for the algorithm that you think can’t be beaten by any algorithm.
For example, printing all elements in a list has a BCR of O(n), since you have to “touch” every element at least once. This is often the BCR for a problem, just “how long does it take to look at all of the items”
It’s not even necessarily a runtime that you think can be achieved (making the name a bit misleading), it’s just a runtime that you think we definitely can’t beat.
SWE: When trying to optimize a problem, what is a possible use for the best case runtime, or BCR, when we have both a BCR and a current, slow solution available?
You have the big O of your current solution, and the big O of the best-case runtime, and you know that the solution must fall somewhere between these two big O’s. So, you can brainstorm possible runtimes between these two big O’s.
If it’s between O(n^2) and O(n), maybe brainstorm how to get it to O(n log n). If our current solution is basically two O(n) processes multiplied together, how can we turn one of those into an O(log n) process?
Suppose we then get it to O(n log n), and our new goal is now O(n), since that’s the BCR. We now know that we probably need to take the O(log n) part to constant time; how do we do that?
But, there is risk with spending too much time searching for a solution with a specific runtime due to process-of-elimination. Solutions sometimes have weird runtimes: maybe it’s O(nloglogn), or maybe there’s some subset of n called k and it’s O(nk), or O(k^2 log n). We don’t want to be blinded from finding these solutions. That said, this can still be a useful tool for thinking. How do I get closer to the BCR, knowing that I can’t actually beat the BCR? Can I try to take x mechanism in my algorithm from y runtime to z runtime?
SWE: If you’re presented an interview question you’ve already seen, should you tell your interviewer?
Yes. If you don’t, it might come off as dishonest.
SWE: A couple code writing tips, flip
Use data structures liberally. If your algorithm needs to deal with objects that have several parts, it’s likely you should make a class.
Write modular code. Try to make a lot of your processes into functions, helper functions, sub-functions, etc. It decreases reused code, helps with testing for errors, and improves readability and prettiness of code. Relatedly, don’t rewrite code more than once, put it in a function.
Don’t get discouraged or overwhelmed if you can’t find the optimal solution. A lot of these questions are designed to be difficult for strong applicants, and many people won’t find a perfect, bug-free solution and will still have done well. Stay calm, keep brainstorming, and try to use your different techniques to keep improving your solution.
Check your function inputs. Rather than assuming your function gets the input in the format it’s looking for, check for the format, and have the function raise errors or return NaN or -1 if format is incorrect.
Write neatly on the board.
(Say your understanding here was 4, so it comes up more.)
SWE: In bit manipulation, given two binary numbers x and y, what are the common symbols for x and y, x or y, x XOR y, and not x?
And: x & y
Or: x | y
XOR: x ^ y
Not: ~x

SWE: How are positive and negative numbers calculated and stored in binary?
When we store binary values in memory, the first bit (meaning the leftmost bit) denotes a number’s sign: if a binary number starts with 0, it’s positive, and if it starts with a 1, it’s negative. (Note that some places do it the other way around, but it’s not a huge dea, you’d just switch it.)
The rest of the digits describe the value of the number. For positive numbers it’s normal binary, so 0100 is 4, for example.
How do we represent negative numbers? Using two’s complement. Specifically, the number is represented with the binary representation of the two’s complement of the absolute value of the number. So if we’re representing -3, the digits (except for the leading 1 denoting sign) are the two’s complement of 3.
SWE: How do we find the two’s complement of a binary number K for the purposes of storing -K, and where do we get this definition from? How would this work for the example of representing -3 if you have 4 total bits available to represent numbers?
From various sources “The two’s complement of an N-bit number K is the complement of a number with respect to 2N; it is the number X such that K + X = 2N”
This can be confusing because here, N-bit number doesn’t mean the number of bits needed to represent the number, it’s the number of available bits that the computer uses to store any integer, minus the sign bit. So of your computer is storing 16-bit integers, then one of those is the sign so they’re really 15-bit integers, so the two’s complement of K is X such that K + X = 215.
Lastly, we can quickly calculate the two’s complement of K by flipping all the bits and adding 1.
For example, in the following table, we’re representing values between +7 and -7 as 4-bit numbers, meaning we have 3 bits for the number and 1 for the sign, so here N = 3.
So, say we’re trying to represent -3 in binary. Now K=3, and for K = 3, the two’s complement is X such that 3 + X = 23 = 8.
So the two’s complement of 3 is 5, and thus the representation for -3 is going to be the representation for 5, plus a 1 at the beginning for sign.
To find this, we can either know of the top of our head that 5 is 101, or we can do it by flipping the bits in 3 and adding 1. This is more scalable for when you have lots of digits, and also you can implement it in code.
3, when you have 3 digits to represent it is 011; flipped that’s 100, and adding 1 you get 101, which is 5, the two’s complement. Tacking on a 1 at the beginning for sign, you have 1101, the binary representation of -3.

SWE: In binary, how does a left shift work? What is k << n? What is 101 << 1?
In a left shift, you just shift all the values over by the listed valeus and fill in zeroes after.
So 101 << 1 is 1010
111 << 3 is 111000.
SWE: In binary/bit manipulation, what is a simple way to multiply a number by 2? What about by 4?
In base 10, you can multiply a number by 10 by adding a zero at the end; for multiplying by 100, you can add two zeroes; etc.
It’s the same in binary. To multiply by 2, simply left shift by 1, filling in a 0 after. To multiply by 4, left shift by 2. To multiply by 32, bit shift by 5, as 25 = 32.
SWE: What are two ways to think about multiplying numbers in binary; for example, 1001*101
The first is to just use the gradeschool base 10 algorithm, but just in binary. In the base 10 algorithm, you multiply the top number by each of the digits in the bottom number, and you add an extra zero in every row. You do this here, remembering that 1*1 = 1, 1*0 = 0, and 0*0 = 0. There’s no carrying or anything. This is shown in the example below.
But, you can also use this idea that to multiply by a power of two 2N, you can just shift left by N bits. So you can also take each of the digits, which are 2N numbers, do all of those shifts, and then add them up. This is exactly what we’re doing in the grade school algorithm, but a different way of doing it. This is nice because we can recognize tricks quickly and save ourselves work. To multiply 1111111 by 10000010 would take a while, until you realize you need to just do two bit shifts, and add those two results.

SWE: How is a string of 0’s often notated in binary? A string of 1’s?
“0s” and “1s”
SWE: What is ~0? What about ~10? How is context important?
What is 1001 & (~0 << 2)?
When we negate numbers, we negate all bits, including all of the zeroes at the beginning of short numbers. So ~0 is a string of 1’s, notated 1s, and ~10 is 1…….101.
Context is important because you do as many preceding zeroes as your computer would use to represent numbers; so for 16-bit numbers (not leaving a bit for sign), we have as many as 16 zeroes to flip. But often, in little problems, we assume that there are infinite zeroes being flipped.
1001 & (~0 << 2)
= 1001 & (1s << 2)
= 000…0001001 & 111……11100
= 1000
SWE: What are the two potential ways of right-shifting a values,
X >> K?
The most common way is to shift all bits to the right, and fill in with 0’s after.
This basically floor divides by 2, or by some other power of 2, for positive numbers: 11111 is 15, and 11111 >> 2 is 111, or 7.
But for negative numbers, it’s weird. 1011010 is -75; right-shifted 1 it’s 0101101, which is 90.
The second way to bit shift is to fill in with 1s after. So 1011010 becomes 1101101. This is good for negative numbers, because it basically ““ceil-divides” them. 1011010 is -75, and 1101101 is -38.
These methods are called “logical right-shift” and “arithmatic right-shift” respectively.
SWE: Given a binary number N, how do we get the value of the ith bit? Here the 1’s place is the 0th bit, the 2’s place is the 1st bit, etc.
We first AND N with a string S that is all 0’s except for a 1 in the ith bit; the result will be a string of 0’s with a 1 in the ith bit iff N has a 1 there. (You can generate S by bitshifting 1 to the left until you have S.)
Then, we just compare the result to 0: if it equals 0, then the ith bit was 0, otherwise it was 1.

SWE: In bit manipulation, what is a mask, and how is it used?
A mask M is a way to get the values of only specific digits in a number N, by setting the rest of them to 0. You do this by ANDing N with the mask M.
Say we only want the 0th, 2nd, and 4th digits of N (counting from right to left). Our mask is then 10101, and we take N & 10101. Because digits 1 and 3 are zeroes, when we and them, they are automatically 0 in the resulting number, regardless of those digits’ values in N.
SWE: How do we set the ith bit of a binary number to 0? How do we set it to 1? Assume in either case that we don’t presently know whether the bit’s value is 0 or 1.
How would we set multiple bits to 0, or multiple bits to 1?
To set it to 0, AND it with a string like 1111101111, where the ith value is 0.
To set it to 1, OR it with a value like 00001000, where the ith value is 1.
Setting multiple is the same: if you’re setting multiple bits to 0, make a string of 1’s where the bits in question are 0’s, and AND. If you’re setting to 1, bame a string of 0’s where the bits in question are 1’s, and OR.
SWE: How do we set the ith bit of binary number N to value v, where v is a variable that might contain 0 or 1?
Clear the ith bit of N by anding it with a number like 11110111, where the ith bit is a 0.
Then, bit shift v until the value of v is in the ith bit.
Lastly, add the masked version of N to the bit-shifted version of v.
SWE: How does a MapReduce program work for analyzing data? What does the programmer need to implement, and then how does the computer resolve the MapReduce program?
How does this work on the common example of counting the number of appearances of each word in a dataset of words?
A MapReduce program takes a dataset containing many points (or just a set of objects containing many objects).
It first maps each data point to a pair. Then, it takes all of the pairs with the same key and “reduces them” in some way, emitting a new, single pair.
As a programmer, you just need to implement a map() function and a reduce() function that makes sense for your use case. The reduce function takes only two values, like in 210; it doesn’t take the whole list of values you need to reduce. You reduce a list by continually reducing pairwise, which is what the machine will do. This is important to note in many cases when considering how to implement the reduce.
(It’s often helpful to first think about how to implement the reduce step, and what that needs to be like, and then figure out the map step based on that.)
The computer first splits the data across several machines, or processors. Each processor runs the map() function on each of its points. Then, the computer does an automatic “shuffle” of the pairs, where each pair with the same key is on the same processor. Lastly, each processor reduces the pairs with the same key using the reduce() function.
For the example where we’re counting the number of appearances of a word, we map a word to , and reduce the pairs by summing the 1’s and keeping the word as the key. This is shown visually, executed by the computer, below.

SWE: At a high level, why is the MapReduce method of solving problems useful in practice?
It allows you to parallelize your data processing. At each step in your processing, you’re using multiple computers rather than just 1. This helps with speed and improves scalability.
Take the example of counting the words in a dataset of words. We could easily just send all the words to a hash table keeping track of number of appearances, but this is an iterative solution. Using a parallelized solution, we can do it faster.
SWE: What is the work and span of an algorithm? At a high level, how do you find an algorithm’s work and span?
The work of an algorithm is its time complexity with one processor; the span of an algorithm is its time complexity with infinite processors, or when it is maximally parallelized.
To find the work, you count up the total actions that need to be done by one processor.
To find the span, you find the longest chain of dependencies, or chain of work. You find the longest sequence of actions that must be done in a specific order, with each action waiting for previous actions to be completed before executing.
SWE: What is a brute-force solution at a high level?
If you’re looking for an answer of a specific type, you try every answer of that type and see which is the best.
For example, the brute force solution for the shortest path problem is to try every possible path and see which is shortest.
The brute-force solution is often a useful naive/baseline solution on which you try to improve.
SWE: At a high level, what is a divide-and-conquer algorithm?
You solve a problem by splitting it into n sub-problems, solving each of the sub-problems (typically in parallel), and then combining the sub-problem answers to get an answer for the original problem.
Often, we split into two sub-problems. We typically want the sub-problems to be of roughly equal size in order to get certain speed-up benefits.
Mergesort is an example of a divide-and-conquer algorithm, and is also an example of why you want roughly equal subproblems.
SWE: At a high level, when trying to find a solution of size n (for some definition of size), what is a greedy algorithm?
In a greedy algorithm, you “greedily” choose the first element that is best at this step, then the second that is best at that step, and so on until you have a size n solution.
Greedy algorithms are a common way of implementing approximation algorithms for maximization problems. Rather than looking at exponentially many possibilities, you approximate such a brute-force solution by doing a greedy algorithm.
If bit ops end up being pertinent, go back to 213/datalab and make some cards to remember useful tricks: negation is ~a+1, multiply by 2 is << 1, floor divide by 2 is >> 1, using masks, etc
…


