Surds

Question 1

When simplifying a surd what do you look for?

Example: simply the square root of 27

Answer 1

Question 2

Important fact: What happens to the surd if you square it?

( √ 5 )²

Answer 2

It dissappears

√ 5 x √ 5 = 5

Question 3

Rules 1

1. When you add and subtract surds they need to be like surds
2. if they are not like surds , look to simplify first

Answer 3

1. 5√ 2 - 3√ 2 = 2√ 2
2. √ 8 - √ 2 = √ 4x√ 2 - √ 2

= 2√ 2-√ 2

=√ 2

Question 4

Rules 2

1. when multiplying with surds - multiple numbers and surds seperately
2. when multiplying surds in brackets use the FOIL method (same as algebra)

Answer 4

1. 2√ 5 x 3√ 3 = 6 √ 15
2. (2√ 3 + √ 5)(√ 5 + √ 2) = 2√ 15 + 2√ 6 +5 √ 10

Question 5

Working backwards

express in terms of √ n

Example: 5√ 2

Answer 5

5√ 2 = √ 25 x √ 2

= √ 50

Question 6

1. Simple

What does rationalising the denomiator mean?

Example 1/ √ 2

Answer 6

the numerator has to be a whoile number

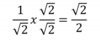
Question 7

2. Harder rationalising the denominator

NB: use the fact of difference of two squares

(√ 5