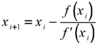stuff

Question 1

what must be true when you are multiplying matrices?

Answer 1

The number of columns is equal to the number of rows

Question 2

What does the determinent represent?

Answer 2

The ratio of the change of area when a matrix is multiplied by a shape.

Question 3

If matrix A provides the transformation B and matrix Y has the transformation Z, what matrix would transform by B and then Z?

Answer 3

Matrix Y* matrix A

Question 4

What is the transpose of a matrix?

Answer 4

Shown by M^t

Question 5

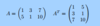
Which way are elements numbered in a matrix?

Answer 5

Question 6

A 6x5 matrix is what size?

Answer 6

6 rows and 5 columns

Question 7

If you have two vectors defining a quadrilateral, how do you find the area?

Answer 7

Cross product the two together and find magnitude

Can be used to find the area of triangles by then dividing by two.

Question 8

How might you find the cross product of two vectors?

Answer 8

Produce a matrix with i,j and k going down the side, and the vectors in centre and right. Find the determinant

Question 9

How do you find the moment of a force?

Answer 9

position X force

Question 10

How can you add matrices of different sizes?

Answer 10

add 0s to make up space.

Question 11

When doing row operations on a matrix, what should a₁₁ be?

Answer 11

Swap rows to ensure it isn’t 0

Life is made easier if it =1

Question 12

When performing row operations, what is the aim?

Answer 12

Ensure the bottom row has two coefficients =0

Question 13

What can you do with row operations?

Answer 13

Change the order of coefficients in a row.

Create new rows by adding them together in combinations

Question 14

When do you use seperation of variables?

Answer 14

dy/dx=f(x)

∫dy=∫f(x) dx

Question 15

How do you use an intergrating factor?

Answer 15

The question will ask for a general solution.

The equation is of the form dy/dx+P(x)y=Q(x)

ln(I)=∫P(x) dx

Multiply the whole equation by I

Integrate both sides. The left hand side should become Iy. Complete the intergration on the right hand side and re-arrange accordiningly.

Should have a C in the final answer unless you are given a point it goes through

Question 16

What is the general form of a second order Homogeneous ODE?

Answer 16

For it to be homogeneous, f(x)=0

Question 17

How do you find the characteristic equation of a _{SECOND ORDER HOMOGENEOUS ODE} ?

Answer 17

Question 18

If the two roots of a characteristic equation of an ODE are real and distict, what does it mean?

Answer 18

y(x)=Ae^r1x+Be^r2x

r₁ and r₂ are the roots of the equation and A and B are constants that are subject to the boundary conditions.

Question 19

If the two roots of a characteristic equation of an ODE are real and the same, what is y(x)

Answer 19

y(x)=Ae^rx+Bxe^rx

Where r is the root and A&B are constants subject to the boundary conditions

Question 20

If the two roots of a characteristic equation for ODE are complex, what is y(x)?

Answer 20

The roots will be of the form p±qi

y(x) = e^px(Acos(qx) + Bsin(qx))

Where A and B are constants subject to the boundary conditions.

Question 21

What is an Inhomogeneous Second Order ODE ?

Answer 21

Question 22

What are the two steps needed to solve an Inhomogeneous Second Order ODE ?

Answer 22

Look at the left hand side, find the characteristic equation and solve as normal to get y_c(x)

Look at the right hand side and chose a particular integral. Substitue it with its derivitives into the orginal equation to find constants. This gives y_p(x).

Add y_c(x) and y_p(x)

Question 23

What are the particular integrals for the following functions?

Answer 23

Question 24

How do you use euler’s method?

Answer 24

Have four columns x, y dy/dx and y_n

Question 25

How does newton-raphson work?

Answer 25

Then feed the result back into it untill you get the precision you want.