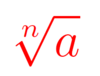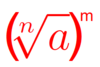Study Sheet Flashcards
Factor: a²-b²
(a+b)(a-b)
Factor: a³+b³
(a+b)(a²-ab+b²)
Factor: a³-b³
(a-b)(a²+ab+b²)
Slope Formula
At an x intercept, what is y equal to?
0
At a y intercept, what is x equal to?
0
What is the equation for the standard form of a line?
Ax+By=C
Note:
m = -A/B
x intercept = C/A
y intercept = C/B
What is the equation for a line in slope-intercept form?
y=mx+b
Note:
m = slope
b = y intercept
What is the equation of a line in point-slope form?
(y-y1)=m(x-x1)
Note:
(x1, y1) is a point on the line
Parallel lines have the same…
Slope
Note:
All vertical lines are parallel.
Perpendicular lines have slopes which are…
Negative reciprocals of each other.
Note:
Their product is -1.
What are two lines with the same slope, but different y intercept called?
Parallel
What are two lines with the same slope, and same y intercept called?
Coincident
What are two lines that are negative recipricals called?
Perpendicular
What are two lines with different slopes, but not negative reciprocals called?
Oblique
Distance Formula
Midpoint Formula
Note:
(x1,y1) and (x2,y2) are points.
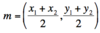
Quadratic Formula
Note:
If ax2+bx+c=0
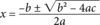
What is the equation of the discriminant?
What does the discriminant do?
b2-4ac
It determines the number and nature of the roots.
If the value of the discrimnant is positive then how many roots of what nature are there?
2 real
If the value of the discriminant is zero then how many roots of what nature are there?
1 real (double root)
If the value of the discriminant is negative then how many roots of what nature are there?
2 imaginary or complex
How do you find the sum of the roots in a discriminant?
-b/a
How do you find the product of the roots in a discriminant?
c/a
am+an=
am+n
(am)n=
amn
a-n=
1/an
1/a-n=
an
(a/b)m=
am/bm
am/an=
am-n
a1/n=
am/n=
General form for a conic section:
Ax2+By2+Cxy+Dx+Ey+F=0
In which conic section is the locus (set) of all point a given distance (radius) from a given point (center)?
Circle
General form for a circle:
Ax2+Ay2+Dx+Ey+F=0
Note:
A=B, C=0
(h, k) form for a circle:
(x-h)2+(y-h)2=r2
Note:
Center- (h,k)
Radius- r
Identify this conic section.
Parabola
In which conic section are the locus of all points whose distance from a given point (focus) and a given line (directrix) equal?
Parabola
Quadratic in x: axis of symetry parallel to the x-axis - Which ways can it open?
Up or Down
General form for a parabola (in x):
Ax2+Dx+Ey+F=0
y=ax2+bx+c
Note:
A and E are nonzero.
a is nonzero.
Vertex form for a parabola (in x):
(x-h)2=4p(y-k)
Note:
Focus: (h,k+p)
Directrix: x=k-p
Quadratic in y: axis of symmetry parallel to the x-axis -
Which ways can it open?
Right or Left
General form for a parabola (in y):
By2+Dx+Ey+F=0
x=ay2+by+c
Note:
B and D are nonzero.
a is nonzero.
Vertex form for a parabola (in y):
(y-k)2=4p(x-h)
Note:
Focus: (h + p,k)
Directrix: x=h-p
Vertex of a parabola:
(h,k)
The distance from the vertex to Focus in a parabola:
p=a/2
The distance from the vertex to Directrix in a parabola:
p
The length of the latus rectum in a parabola:
4p
