Structure of Matter

Question 1

Matter can be distinguished in two forms. What are they? Give four examples of each. Give two examples of mutual transformation.

Answer 1

Particles: Solid, Liquid, Gas and Plasma Phase

Fields: Gravitational, Electromagnetic, Strong Nuclear and Weak Nuclear. *Matter can mutually transform e.g annihilation of particle with its antiparticle –> EM radiaiton (particle –> field)

Example of opposite transformation is the absorption of gamma-radiation to create electron-positron pair.

Question 2

What are the names of the two groups of fundamental particles (corpuscular matter)? Name on key difference between them.

Answer 2

Leptons DO NOT interact with the strong nuclear force. Quarks do.

Question 3

What are the three different generations of Quarks and state their charges? Describe the property COLOUR

Answer 3

Quarks generations differ according to a property called FLAVOUR: 1) down (-1/3) / up (+2/3) 2) strange (-1/3) /charm (+2/3) 3) bottom (-1/3) /top (+2/3) Each quark has a further property called ‘colour’, which can be: Red, Blue or Green.

Question 4

What are the different FLAVOURS of Leptons?

Answer 4

1) electron / electron neutrino 2) muon / muon neutrino 3) tau / tau neutrino

Question 5

What is meant by corpuscular-wave dualism?

Answer 5

Every elementary particle (i.e particle with unknown substructure) possesses (as do their systems: atoms, molecules) particle and wavelike properties. Light produces interference and diffraction patterns, only explanation is that waves interfere CONSTRUCTIVELY and DESTRUCTIVELY producing alternating bands of dark and light.

Diffraction patterns are observed when accelerated electrons in a vacuum tube interact with the spaces in a graphite crystal. The spread of lines in the diffraction pattern increases if the wavelength of the wave is greater. Slower electrons give widely spaced rings. –> if v is greater, wavelength is shorter and spread of lines is smaller.

Photoelectric effect demonstrates that light is a flux of energy in the form of photons.

Question 6

Louis de Broglie asserted what? State his equation

Answer 6

“If ‘wave-like’ light showed particle properties (photons), ‘particles’ like electrons should be expected to show wave-like properties.”

λ=hv/mv²=h/mv

Where… λ = wavelength (m), h = Planck’s constant (6.63 × 10^(-34) Js), mv = mass x velocity (= momentum = p = Kg.m/s)

and… f = frenquency (Hz), E = energy (J). Elementary particles have very short wavelengths –> electron microscope better than light.

Question 7

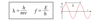
Explain the Heisenberg Uncertainty Principle? Give the equation that explains the relationship between the momentum of a photon and the speed of light.

Answer 7

It is impossible to determine with perfect accuracy the position and momentum of a particle simultaneously. If the position of vector r is being measured its momentum will change, and visa versa.

p = hv ∕ c = h / λ

where c = speed of light = roughly 3 x 10^8 m/s

Question 8

In what form is electromagnetic radiation emitted? State the equation to determine a value for this energy? How does this suggest a particulate nature of EM radiation?

Answer 8

Energy emitted from EM radiation comes in discrete bundles called ‘quanta’.

E=hf=hc/λ

This suggests a particulate nature of EM radiation because each photon contains energy proportional to its frequency.

High frequency (short wavelength) = high energy

Low frequency (long wavelength) = low energy

Question 9

What is meant my the ‘state’ of an electron, and how can it be described? What is the WAVE FUNCTION? Describe the Pauli Exclusion Principle? What is the purpose of Quantum Numbers, what are they?

Answer 9

The state of an electron refers to its energy and position in the orbital. The electron state is described by the wave function involving a number of dimensionless parameters, which equal the number of degrees of freedom = 4.

All four Quantum numbers determine the state of an electron, with the exception of spin, these numbers determine the geometry and symmetry of the electron cloud.

Pauli Exclusion Principle - no two electrons in a given atom can share the same quantum numbers.

1. Principal Quantum Number (n)

2. Orbital Quantum Number (l)

3. Magnetic Quantum Number (m)

4. Spin Quantum Number (s)

Question 10

Describe the first two Quantum numbers?

Answer 10

Principal Quantum number (n) - describes the main energy level, in which the electron is present in its ground state. Values of n range from 1-7 ( aka K-Q). As n increases e^- tend to be further from nucleus and have higher potential energy. Electrons with the same principal quantum number tend to be in the same electron shell. Max no. of e^- in any shell = 2n² (i.e 1^st shell 2x1² = 2).

Orbital or ‘subshell’ quantum number (l) - is used for notation of states in spectroscopy - (study of interaction of matter with EM radiation), it determines form and symmetry of electron cloud and describes the subshell of the electron (it describes the shape of the orbital). For any given n, l = any number from 0–> n-1. l is determined by the angular momentum L where the magnitude of L is given by the equation:

L = h√l(l+1)

values of l = 0,1,2,3,4,5 corresponds to s,p,d,f,g

Question 11

Describe the last two Quantum numbers? What is meant by allowed or forbidden transitions?

Answer 11

Magnetic Quantum Number (m_l) - can possess values: 0, ±1, ±2… ±l for given l (so no. of possible values for m_l = 2l+1) . It determines the spatial position of the orbital. m represents the number of possible values for available energy levels of that subshell. It specifies the exact orbital within the subshell where an electron can be found. It also describes the direction of the angular momentum vector (L) in an external magnetic field.

Spin Quantum Number (m_s) - can possess values: ±½. Each electron possesses its own, internal angular momentum, which does NOT depend on its orbital angular momentum. In presence of external magnetic field, e^- orientate themselves in one of two possible positions:

+1/2 - counter-clockwise spin

-1/2 - clockwise spin

During e^- transitions due to absorption or emission of energy, quantum no. (n) can vary arbitrarily.

Allowed (probable) transition = orbital quantum no. (l) varies by no more than ±1

Forbidden (improbable) transition = orbital quantum no. (l) varies by more than ±1

Question 12

What are Fermi particles?

What’s the equation that describes orbital magnetic moment of an electron?

Answer 12

Fermi particles have a half value of spin. Bosons have integer spin values.

μ_{B =} Orbital magnetic moment of an electron. Unit μ_B = Bohr Magnetron

μ_B = E_Binding + ½ m.v² = eh/2me = 927,900,968 (J/T)

me = resting mass of e^- = 9.11×10^-31 Kilograms

e = elementary charge = 1.602 x 10^-19 Coulombs

h = Planck’s constant = 6.626 x 10^-34 Joule Seconds

Question 13

What is the Heisenberg’s relation of uncertainty? What are Fermions and Bose particles (bosons), give examples of both? Define angular momentum L? State Dirac’s constant, and how is it derived?

Answer 13

Dirac’s constant: ħ = h/2π = 1.05 x 10^-34 (J.s)

Angular momentum (L) is defined as a vector cross product of vector r and of vector of momentum p = mv.

L = [r x p]

NB: vector product of two vectors is a vector perpendicular to plane determined by the vectors multiplied, and its magnitude = the product of their magnitudes multiplied by the sine of their angle.

Particles with half-value of spin are called Fermi particles (fermions) while those with integer values of spin are called Bose particles (bosons) e.g electron is fermion, while photon is boson.

Heisenberg’s relation of uncertainty holds for the uncertainty of the position of vector r and p:

Δr x Δp ≥ ħ…thus smaller region of motion results in higher uncertainty of momentum.

Question 14

How do you calculate the potential energy and the kinetic energy of an electron in the field of a proton? thus total energy of electron in the field of one proton = ? What is Bohr’s radius?

Answer 14

E_k = p²/2m_e = ħ²/2m_er²

E_p = - 1/4πε_{0 .} e²/r

E = E_{k +} E_p

m_e = 9.1 x 10^-31 Kg

ε_{0 =} 8.8 x 10^-12 F.m^-1 = the absolute dielectric permittivity of classical vacuum.

Bohr’s radius - r₀ = 4πε₀ħ²/m_ee² = 5.29 x 10^-11 (m) = the allowed radii for electrons in circular orbits of the hydrogen atom

The Bohr radius, symbolized a , is the mean radius of the orbit of an electron around thenucleus of a hydrogen atom at its ground state (lowest-energy level).

Question 15

What happens when an electron that has been excited to a higher energy level falls back down to its ground state? How do you calculate the frequency or wavelength of this radiation? What is a Line Spectrum?

Answer 15

As the electron falls back down to its ground state it emits a photon. The energy of this photon (E) =

E = E_k - E_n

Where, E_k = energy of electron in elevated state

and… E_n = energy of electron in ground state.

Frequency and wavelength: E = hf = hc/λ

Line Spectrum = graphical depiction where each line corresponds to a specific electron transition. The set of spectral lines observed during transitions from all higher levels into a certain energy level corresponding to a given n is called a series.

Question 16

The atomic emission spectra of hydrogen is composed of several series. What are they? What are the different wavelengths for the three ‘types’ of light?

What is Hund’s rule?

Answer 16

The Lyman Series - Transitioning into the basic energy level n = 1, observed in the UV spectrum (10-380nm).

The Balmer Series - Transitioning into n = 2, observed in visible light spectrum (380-790nm).

The Paschen Series - Transitioning into n ≥ 3, observed in infrared region of light spectrum (>790nm).

Greatest energy photon emitted MUST be from Lyman Series as is biggest fall in energy.

Hund’s rule - if possible electrons remain unpaired, –> they possess parallell spins.

Question 17

How can an electron achieve an excited state? What are the conditions for this kind of quantum transition?

Answer 17

Absorption of a photon.

The energy absorbed MUST equal the energy difference between the excited and ground states of the electron.

Question 18

What is Ionisation? Discuss the energy of an electron in a system (an atom), and binding energies of different atoms.

What is Einstein’s equation for the photoelectric effect?

Answer 18

Ionisation occurs when an electron absorbs energy (E = hf) greater than its binding energy (the energy required to remove an electron from its atom)

Energy absorbed must overcome electrostatic forces holding the electron to the nucleus.

Total energy of an electron in the system of a nucleus is negative. Highest possible energy = 0 in a system where n = ∞ and r = ∞ so… E_b + E = 0 …so… E_b = -E

E = E_b + Ek

Binding energy (E_b ) AKA Ionisation potential of an electron in the field of a nucleus is positive and equals its total energy.

Ionisation potential varies:

Valence electrons have the lowest values.

Heavy atoms like uranium Z = 92, have much higher binding energies (Z² times higher than H e^-)

Ionisation forms cations, but they are not stable as losing electron increases energy of system so atom tends to return to ground state with simultaneous emission of fluorescent radiation.

Photoelectric effect:

hf = E_b + ½mv^{<strong>2</strong>} - many metals emit electrons when light shines on them, but only by photons that reach or exceed a threshold frequency.

Question 19

What is Luminescence?

Answer 19

Luminescence is the emission of light by a substance not resulting from heat. Radiation transitions of electrons from higher into lower energy levels results in luminescence.

Question 20

Discuss the structure of electron shells in atoms. What is meant by electron configuration?

Discuss three principles by which the electron configuration of an element can be determined.

Answer 20

Electron configuration is the most stable arrangement of electrons in the atom i.e the one having least energy.

Electron structure - Quantum-mechanical (wave-mechanical) model currently accepted. Theory advocates e^- moving in ‘cloud’ surrounding nucleus. Electrons have properties of mass particle and wave simultaneously. Movement of e^- characterised by wave function (ψ - psi). Energy of e^- is quantized meaning electrons only appear in specific energetic states. The areas in which it’s ‘more likely’ to find electrons with a specific energetic content are called orbitals. Orbitals can be defined as the √ψ

The building up or Aufbau principle - electrons are added to orbitals in the order of increasing energy i.e the following sequence:

1S², 2S², 2P⁶, 3S², 3P⁶, 4S², 3D¹⁰, 4P⁶, 5S², 4D¹⁰, 5P⁶, 6S², 5D¹⁰, 4F¹⁴, 6P⁶…

The Pauli Exclusion Priciple - No two electrons in one atom can have the same four quantum numbers.

The Hund’s rule - Orbitals of equal energy (degernerate orbitals) are occupied by a single electron before pairing occurs.

Question 21

Atomic Nucleus:

• Atomic number ​Z*
• Mass number A*
• Neutron number N*

what are isotopes, isobars and isomers?

Answer 21

Nucleon = protons and neutrons.

A = Z + N

Total electric charge of nucleus = Z x 1.6x10^-19 C.

Nucleon mass roughly 2000 x greater than electron mass.

Atomic Mass Unit (AMU) = 1/12^th the mass of a C-12 atom = 1.66 x 10^-27 Kg = 931 MeVm mass of atom estimated using mass spectrometry

Isotopes - same Z, different N

Isobars - same A, different Z

Isomers - same Z and N but have nuclei of different energy levels. So they’re not stable, e^- fall back to ground states and emit radiation.

Radius of a proton = 1.23 x 10^-15 m … radius of heavy atoms can be calculated R_a = 1.23 x 10^-15 m x A^1/3

Atomic radii decreases from left to right and increases down a group

Nuclear forces hold an atom together via the strong interaction: range = 10^-15 m, strength NOT dependent on nuclear charge. This strong interaction is the strongest force in nature at this distance.

Question 22

Discuss the binding energy of the atomic nucleus and explain Mass Defect (Δm).

Answer 22

Binding energy of atomic nucleus determines its stability, it = work that must be done to remove particle from system. E of e^- = -ve value, at its highest value were n = infinity and r also = infinity E = 0, so E_b + E = 0 therefore, E_b = ^-E. Thus law of energy conservation = Einstein’s photoelectric effect = hf = E_b + ½mv²

Mass defect (Δm) is the difference between the theoretically calculated and actually measured mass of the nucleus. In theory m_nucleus should = Zm_p + Nm_{<strong>n</strong>.} But mass of nucleus is always less than the combined mass of its protons and neutrons. This difference is due to matter that has been converted to binding energy which holds nucleon together. A greater mass defect results in greater binding energy.

Iron has greatest binding energy and is most stable atom. General rule, intermietely sized atoms most stable.

Question 23

What is meant by ‘potential barrier of atomic nucleus’, list three positively charged particles in your answer.

Answer 23

At very short distances (1 femtometer), strong interactions are about 100 x stronger than electromagnetic interactions. Electric charge of nucleus forms an electrostatic force field around it with a potential U(r) that is a function of the distance r from nucleus. Thus a potential barrier exists due to the electromagnetic interaction for positively charged particles (proton, deutron and α-particle) that enter the nucleus.

Question 24

What are the physical principles behind mass spectrometry?

• 4 stages

1 equation with 2 parts

Answer 24

Mass spectrometry is used to determine the isotopic composition of a sample. The method relies on the simple fact that the trajectory of charged particles in a magnetic field is dependent on the particles mass. Mass spectrometry works by the following procedure:

1. Sample is ionised (electron removed) to become cation with charge q
2. the ions (with charge q) are accelerated in a longtitudinal electric field with a potential difference of U where E = qU. This forms a beam of ions.
3. The ion beam is separated into several beams depending on each ions specific charge = q/M. The degree of deflection is dependent on mass to charge ratio.
4. Each beam is detected and intensity is recorded. Intensity provides information about relative amount of each isotope present in the sample (% composition).

E = qU = ½mv²

Where U = potential difference.

Question 25

What are the magnetic properties of atomic nuclei?

Answer 25

Protons and neutrons have their own half-integer angular momentum (spin). The vectors of a proton’s internal magnetic momentum and spin magnetic moment are in the same direction. However, in a neutron they’re anti-parallel.

Magnetic moment of a proton is 658 times lower than that of an electron. Hence why magnetic phenomena of nuclei are so weak.

Nuclei, which contain an odd number of nucleons possess a resulting spin is non-zero. These nuclei also possess a non-zero magnetic moment since protons as well as neutrons are formed by electrically charged quarks. All nuclei composed of an even number of protons or neutrons possess a zero spin.

E.g: zero spin = ¹²C₆, ¹⁶O₈, ³²S₁₆, ⁴⁰Ga_20.

non-zero spin = ¹H₁, ²D₁, ⁷Li₃, ¹³C₆, ¹⁴N₇, ¹⁹F₉, ²³Na₁₁, ¹²⁷I_53.

Product of nuclear spin I and Dirac constant yields spin of nucleus… Iħ = spin of nucleus.

Nuclei with even mass no. have integer values of spin (in units ħ) and nuclie with odd mass no. possess half-integer values for spin. Magnetic moment of nucleus is expressed in units of nuclear magneton (n.m)

1 n.m = eħ/2m_p = 5.05 x 10^-27 J.T^-1

Question 26

Discuss the physical principals behind nuclear Magnetic Resonance Tomography.

Answer 26

The magnetic properties of atomic nuclei provide the basis for NMRI techniques.

Magnetic moment of proton = 2.8nm and neutron = 1.9nm. All elements have at least one isotope with a nucleus with a magnetic moment. Only when no. of both protons and neutrons in nuclide is even is there no spin.

Potential energy of nucleus / proton in presence of external magnetic field B = μB where μ = magnetic moment of the proton.Protons can exist in two possible energy states within a magnetic field: ±μB depending on their ±½ spin value. In higher energy states, magnetic moments are oriented antiparallel to the field. Lower energy states, the magnetic moments are alligned WITH the field.

If protons are exposed to EM radiation with energy that equals the difference between these two energy states, resonance exchange of energy occurs between the nuclei and the incident wave.

E = hf = 2μB

ω=2πf … where ω = angular frequency

Resonance exchange of energy is called nuclear magnetic resonance, this resonance exchange of energy occurs at Lamors frequency.

NOTE: if proton is in lower energy state (-μB), a photon is absorbed and transition into higher energy state –> +μB occurs. However, if proton is in a higher energy state (+μB), then a photon is emitted and transition into lower energy state -μB occurs

Question 27

How does an MRI work?

Answer 27

Free protons in the hydrogen nuclei of water are used, since almost all biological tissues contain water.

Patient is placed into an external magnetic field which aligns the magnetic moments of hydrogen nuclei, pulses of radio waves are passed through the patient causing deflection of the magnetic moments, which return to their lower energy states with simultaneous emission of a photon. The strength, frequency, and time it takes for the nuclei to return to their pre-excited state produces a signal. This signal is analyzed by a computer an image is produced in which the differences of tissue composition can be visualized.